
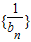 的前n項和為Tn.
的前n項和為Tn.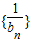 的通項公式及前n項和為Tn的表達(dá)式.
的通項公式及前n項和為Tn的表達(dá)式.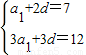

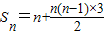 =
=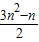 +n=
+n=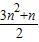
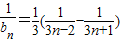
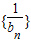 的前n項和
的前n項和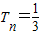 [1-
[1-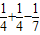 +…+
+…+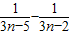
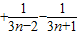 ]=
]=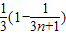
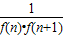 的形式時,常使用裂項法將數(shù)列的一項
的形式時,常使用裂項法將數(shù)列的一項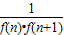 分解為
分解為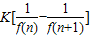 的形式,即裂項求和的應(yīng)用
的形式,即裂項求和的應(yīng)用 

湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com