
(
開放性問題)已知a>0,且a≠1,解關于x的不等式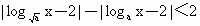 .
. |
解:設  ,則原不等式變為 ,則原不等式變為 . ① . ①
(1) 當t>2時,由①得2(t-1)-(t-2)<2,∴t <2,所以,此時不等式無解.(2) 當1<t≤2時,由①得2(t-1)+(t-2)<2,∴3t <6,∴t<2.∴1 <t<2.(3) 當t≤1時,由①得-2(t-1)+(t-2)<2,∴ -2t+2+t-2<2,∴t>-2,∴-2<t≤1.綜合上面 (1)(2)(3)三種情況可得-2<t<2,即 . .
若 a>1時,有 ,∴ ,∴ . .
若 0<a<1時,有 ,∴ ,∴ . .
因此不等式的解集為: (1) ;(2) ;(2)
|
|
分析:必須去掉絕對值符號,才能求解,可以利用劃分區間的方法.為了使解題的過程更加簡便可以采用變量代換把 |


 王后雄學案教材完全解讀系列答案
王后雄學案教材完全解讀系列答案 海淀課時新作業金榜卷系列答案
海淀課時新作業金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 輕松課堂標準練系列答案
輕松課堂標準練系列答案科目:高中數學 來源: 題型:044
(
開放性問題)已知曲線 的方程為xy=-1,曲線
的方程為xy=-1,曲線 關于點M(
關于點M( ,
, )的對稱曲線為
)的對稱曲線為 .
.
(1)
求曲線 的表達式y=f(x),并寫出y=f(x)的單調區間;
的表達式y=f(x),并寫出y=f(x)的單調區間;
(2)
若a>b>0, ,求證:
,求證: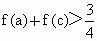 ;
;
(3)
設點N(x,y)在曲線 上運動,且
上運動,且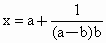 (a>b>0),求點N的縱坐標y的取值范圍.
(a>b>0),求點N的縱坐標y的取值范圍.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com