
設函數f(x)= x3-mx2+(m2-4)x,x∈R.
(1)當m=3時,求曲線y=f(x)在點(2,f(2))處的切線方程;
(2)已知函數f(x)有三個互不相同的零點0,α,β,且α<β.若對任意的
x∈[α,β],都有f(x)≥f(1) 恒成立,求實數m的取值范圍.
見解析
解:(1)當m=3時,f(x)= x3-3x2+5x,f ′ (x)=x2-6x+5.
因為f(2)= ,f ′ (2)=-3,所以切點坐標為(2,), 切線的斜率為-3.
則所求的切線方程為y- =-3(x-2),即9x+3y-20=0.
(2)解法一:f ′ (x)=x2-2mx+(m2-4),令f ′ (x)=0,得x=m-2或x=m+2.
當x∈(-∞,m-2)時,f ′ (x)>0,f(x)在(-∞,m-2)上是增函數;
當x∈(m-2,m+2)時,f ′ (x)<0,f(x)在(m-2,m+2)上是減函數;
當x∈(m+2,+∞)時,f ′ (x)>0,f(x)在(m+2,+∞)上是增函數.
因為函數f(x)有三個互不相同的零點0,α,β,且f(x)=x[x2-3mx+3(m2-4)],
所以解得m∈(-4,-2)∪(-2,2)∪(2,4).
當m∈(-4,-2)時,m-2<m+2<0,所以α<m-2<β<m+2<0.
此時f(α)=0,f(1)>f(0)=0,與題意不合,故舍去;
當m∈(-2,2)時,m-2<0<m+2,所以α<m-2<0<m+2<β.
因為對任意的x∈[α,β],都有f(x)≥f(1)恒成立,所以α<1<β.
所以f(1)為函數f(x)在[α,β]上的最小值.
因為當x=m+2時,函數f(x)在[α,β]上取最小值,所以m+2=1,即m=-1;
當m∈(2,4)時,0<m-2<m+2,所以0<α<m-2<m+2<β.
因為對任意的x∈[α,β],都有f(x)≥f(1)恒成立,所以α<1<β.
所以f(1)為函數f(x)在[α,β]上的最小值.
因為當x=m+2時,函數f(x)在[α,β]上取最小值,所以m+2=1,即m=-1 (舍去).
綜上可知,m的取值范圍是{-1}.
解法二:f ′ (x)=x2-2mx+(m2-4),令f ′ (x)=0,得x=m-2或x=m+2.
所以,當x∈(-∞,m-2)時,f ′ (x)>0,f(x)在(-∞,m-2)上是增函數;
當x∈(m-2,m+2)時,f ′ (x)<0,f(x)在(m-2,m+2)上是減函數;
當x∈(m+2,+∞)時,f ′ (x)>0,f(x)在(m+2,+∞)上是增函數.…9分
當α<β<0時,必有α<m-2<β<m+2<0,則當x∈[α,β]時,f(x)的最小值是f(α)=0.
此時f(1)>f(0)=0=f(α),與題意不合,故舍去;
當α<0<β時,則有α<m-2<0<m+2<β,此時3(m2-4)<0,即-2<m<2.
因為對任意的x∈[α,β],都有f(x)≥f(1)恒成立,所以α<1<β.
所以f(1)為函數f(x)在[α,β]上的最小值.
又函數f(x)在[α,β]上的最小值就是極小值,所以f′(1)=0,得m=3(舍去)或m=-1;
當0<α<β時,則有0<α<m-2<m+2<β,此時
解得m∈(2,4).
因為對任意的x∈[α,β],都有f(x)≥f(1)恒成立,所以α<1<β.
所以f(1)為函數f(x)在[α,β]上的最小值.
又函數f(x)在[α,β]上的最小值就是極小值,所以f ′(1)=0,得m=3或m=-1(舍去).
又因為當m=3時,f(1)為極大值,與題意不合,故舍去.
綜上可知,m的取值范圍是{-1}.


 學而優暑期銜接南京大學出版社系列答案
學而優暑期銜接南京大學出版社系列答案 Happy holiday歡樂假期暑假作業廣東人民出版社系列答案
Happy holiday歡樂假期暑假作業廣東人民出版社系列答案科目:高中數學 來源:2002年全國各省市高考模擬試題匯編 題型:044
設函數f(x)=![]() (x-1)(a>0,且a≠1),當點P(x,y)是函數y=f(x)圖象上的點時,點Q(3x,
(x-1)(a>0,且a≠1),當點P(x,y)是函數y=f(x)圖象上的點時,點Q(3x,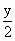 )是函數y=g(x)圖象上的點.
)是函數y=g(x)圖象上的點.
(Ⅰ)寫出函數y=g(x)的解析式;
(Ⅱ)求不等式g(x)≤f(x)的解集.
查看答案和解析>>
科目:高中數學 來源:廣州市2008屆高中教材變式題2:二次函數 題型:022
設函數f(x)=x|x|+bx+c,給出下列4個命題:
①當c=0時,y=f(x)是奇函數;
②當b=0,c>0時,方程f(x)=0只有一個實根;
③y=f(x)的圖象關于點(0,c)對稱;
④方程f(x)=0至多有兩個實根.
上述命題中正確的序號為________.
查看答案和解析>>
科目:高中數學 來源:天津市耀華中學2012屆高三寒假驗收考試數學理科試題 題型:013
設函數f(x)=x|x|+bx+c,則下列命題中正確命題的序號有
①當b>0時,函數f(x)在R上是單調增函數;
②當b<0時,函數f(x)在R上有最小值;
③函數f(x)的圖象關于(0,c)對稱;
④方程f(x)=0可能有三個實數根.
A.①③
B.①④
C.①②④
D.①③④
查看答案和解析>>
科目:高中數學 來源:廣東省云浮羅定中學2012屆高三11月月考數學理科試題 題型:044
已知二次函數y=g(x)的圖象經過點O(0,0)、A(m,0)與點P(m+1,m+1),設函數f(x)=(x-n)g(x)在x=a和x=b處取到極值,其中m>n>0,b<a.
(1)求g(x)的二次項系數k的值;
(2)比較a,b,m,n的大小(要求按從小到大排列);
(3)若m+n≤2![]() ,且過原點存在兩條互相垂直的直線與曲線y=f(x)均相切,求y=f(x).
,且過原點存在兩條互相垂直的直線與曲線y=f(x)均相切,求y=f(x).
查看答案和解析>>
科目:高中數學 來源:2012-2013學年寧夏高三第五次月考理科數學試卷(解析版) 題型:填空題
設函數f(x)= ,D是由x軸和曲線y=f(x)及該曲線在點(1,0)處的切線所圍成的封閉區域,則z=x-2y在D上的最大值為________.
,D是由x軸和曲線y=f(x)及該曲線在點(1,0)處的切線所圍成的封閉區域,則z=x-2y在D上的最大值為________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com