
【題目】數(shù)列![]() 對于確定的正整數(shù)
對于確定的正整數(shù)![]() ,若存在正整數(shù)
,若存在正整數(shù)![]() 使得
使得![]() 成立,則稱數(shù)列
成立,則稱數(shù)列![]() 為“
為“![]() 階可分拆數(shù)列”.
階可分拆數(shù)列”.
(1)設![]() 是首項為2,公差為2的等差數(shù)列,證明
是首項為2,公差為2的等差數(shù)列,證明![]() 為“3階可分拆數(shù)列”;
為“3階可分拆數(shù)列”;
(2)設數(shù)列![]() 的前
的前![]() 項和為
項和為![]()
![]() ,若數(shù)列
,若數(shù)列![]() 為“
為“![]() 階可分拆數(shù)列”,求實數(shù)
階可分拆數(shù)列”,求實數(shù)![]() 的值;
的值;
(3)設![]() ,試探求是否存在
,試探求是否存在![]() 使得若數(shù)列
使得若數(shù)列![]() 為“
為“![]() 階可分拆數(shù)列”.若存在,請求出所有
階可分拆數(shù)列”.若存在,請求出所有![]() ,若不存在,請說明理由.
,若不存在,請說明理由.
【答案】(1)見解析;(2)![]() ;(3)
;(3)![]() 或3.
或3.
【解析】試題分析:
(1)利用題中所給的新定義內(nèi)容結合等差數(shù)列的通項公式即可證得結論;
(2)由題意整理計算可得![]() ;
;
(3)假設實數(shù)m存在,討論可得![]() 或3.
或3.
試題解析:
(1)由題意可知![]()
![]() ,
,![]() 所以
所以![]()
所以![]() 為“3階可分拆數(shù)列”;
為“3階可分拆數(shù)列”;
因為數(shù)列![]() 的前
的前![]() 項和為
項和為![]()
![]()
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]()
所以![]()
因為存在正整數(shù)![]() 得
得![]() 成立
成立
當![]() 時
時![]() 即
即![]()
因為![]() ,
,![]()
所以![]() ,而
,而![]() 所以不存在正整數(shù)
所以不存在正整數(shù)![]() (
(![]() )使得
)使得![]() 成立
成立
當![]() 時
時![]() ,得
,得![]()
所以![]() 時存在正整數(shù)
時存在正整數(shù)![]() 使得
使得![]() 成立
成立
由得![]() .
.
假設存在![]() 使得若數(shù)列
使得若數(shù)列![]() 為“
為“![]() 階可分拆數(shù)列”
階可分拆數(shù)列”
即存在確定的正整數(shù)![]() ,存在正整數(shù)
,存在正整數(shù)![]() 使得
使得![]() 成立
成立
![]()
![]()
當![]() 時,
時,![]() ,
,![]() 時方程成立
時方程成立
當![]() 時
時![]()
當![]() 時
時![]() ;當
;當![]() 時
時![]()
當![]() 時
時![]() ,所以不存在正整數(shù)
,所以不存在正整數(shù)![]() 使得
使得![]() 成立
成立
當![]() 時
時![]() ,當
,當![]() 時
時![]() 成立
成立
④當![]() 時
時![]()
所以不存在正整數(shù)![]() 使得
使得![]() 成立
成立
綜上:![]() 或3.
或3.


 品學雙優(yōu)卷系列答案
品學雙優(yōu)卷系列答案 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案 期末復習檢測系列答案
期末復習檢測系列答案 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案科目:高中數(shù)學 來源: 題型:
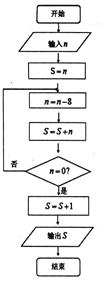
【題目】《孫子算經(jīng)》是中國古代重要的數(shù)學著作,約成書于四、五世紀,也就是大約一千五百年前,傳本的《孫子算經(jīng)》共三卷,卷中有一問題:“今有方物一束,外周一匝有三十二枚,問積幾何?”該著作中提出了一種解決問題的方法:“重置二位,左位減八,余加右位,至盡虛加一,即得.”通過對該題的研究發(fā)現(xiàn),若一束方物外周一匝的枚數(shù)![]() 是8的整數(shù)倍時,均可采用此方法求解,如圖,是解決這類問題的程序框圖,若輸入
是8的整數(shù)倍時,均可采用此方法求解,如圖,是解決這類問題的程序框圖,若輸入![]() ,則輸出的結果為( )
,則輸出的結果為( )
A. 120 B. 121 C. 112 D. 113
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】根據(jù)題意解答
(1)求定積分 ![]() |x2﹣2|dx的值;
|x2﹣2|dx的值;
(2)若復數(shù)z1=a+2i(a∈R),z2=3﹣4i,且 ![]() 為純虛數(shù),求|z1|
為純虛數(shù),求|z1|
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知![]() ,曲線
,曲線![]() 上任意一點
上任意一點![]() 滿足
滿足![]() ;曲線
;曲線![]() 上的點
上的點![]() 在
在![]() 軸的右邊且
軸的右邊且![]() 到
到![]() 的距離與它到
的距離與它到![]() 軸的距離的差為1.
軸的距離的差為1.
(1)求![]() 的方程;
的方程;
(2)過![]() 的直線
的直線![]() 與
與![]() 相交于點
相交于點![]() ,直線
,直線![]() 分別與
分別與![]() 相交于點
相交于點![]() 和
和![]() .求
.求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=(x﹣t)|x|(t∈R).
(1)討論y=f(x)的奇偶性;
(2)當t>0時,求f(x)在區(qū)間[﹣1,2]的最小值h(t).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點 .
.
(1)求![]() 的方程;
的方程;
(2)是否存在直線![]() 與
與![]() 相交于
相交于![]() 兩點,且滿足:①
兩點,且滿足:①![]() 與
與![]() (
(![]() 為坐標原點)的斜率之和為2;②直線
為坐標原點)的斜率之和為2;②直線![]() 與圓
與圓![]() 相切,若存在,求出
相切,若存在,求出![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】比較下列各題中兩個數(shù)的大小:
(1)log60.8,log69.1;
(2)log0.17,log0.19;
(3)log0.15,log2.35
(4)loga4,loga6(a>0,且a≠1)
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com