
【題目】在直角坐標系xOy中,設傾斜角為α的直線: ![]() (t為參數)與曲線C:
(t為參數)與曲線C: ![]() (θ為參數)相交于不同的兩點A,B.
(θ為參數)相交于不同的兩點A,B.
(1)若α= ![]() ,求線段AB的長度;
,求線段AB的長度;
(2)若直線的斜率為 ![]() ,且有已知點P(2,
,且有已知點P(2, ![]() ),求證:|PA||PB|=|OP|2 .
),求證:|PA||PB|=|OP|2 .
【答案】
(1)
解:由曲線C: ![]() (θ為參數),可得C的普通方程是
(θ為參數),可得C的普通方程是 ![]() =1.
=1.
當 ![]() 時,直線方程為:
時,直線方程為: 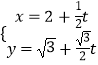 (t為參數),
(t為參數),
代入曲線C的普通方程,得13t2+56t+48=0,
則線段AB的長度為 ![]()
(2)
證明:將直線l的參數方程代入曲線C的普通方程,
化為:(cos2α+4sin2α)t2+(8 ![]() sinα+4cosα)t+12=0,
sinα+4cosα)t+12=0,
∵ ![]()
![]() ,
,
而直線的斜率為 ![]() ,則
,則 ![]() 代入上式求得|PA||PB|=7.
代入上式求得|PA||PB|=7.
又 ![]() ,
,
∴|PA||PB|=|OP|2
【解析】(1)由曲線C: ![]() (θ為參數),利用平方關系可得C的普通方程.當
(θ為參數),利用平方關系可得C的普通方程.當 ![]() 時,直線方程為:
時,直線方程為: 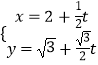 (t為參數),代入代入曲線C的普通方程,得13t2+56t+48=0,利用一元二次方程的根與系數的關系、弦長公式即可得出.(2)將直線l的參數方程代入曲線C的普通方程,化為:(cos2α+4sin2α)t2+(8
(t為參數),代入代入曲線C的普通方程,得13t2+56t+48=0,利用一元二次方程的根與系數的關系、弦長公式即可得出.(2)將直線l的參數方程代入曲線C的普通方程,化為:(cos2α+4sin2α)t2+(8 ![]() sinα+4cosα)t+12=0,利用根與系數的關系即可得出.
sinα+4cosα)t+12=0,利用根與系數的關系即可得出.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】設a為實數,函數f(x)=(x﹣a)2+|x﹣a|﹣a(a﹣1).
(1)若f(0)≤1,求a的取值范圍;
(2)求f(x)在R上的單調區間(無需使用定義嚴格證明,但必須有一定的推理過程);
(3)當a>2時,求函數g(x)=f(x)+|x|在R上的零點個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|x2﹣2x﹣8≤0},B={x| ![]() <0},U=R.
<0},U=R.
(1)求A∪B;
(2)求(UA)∩B;
(3)如果C={x|x﹣a>0},且A∩C≠,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,若對于在定義域內存在實數
,若對于在定義域內存在實數![]() 滿足
滿足![]() ,則稱函數
,則稱函數![]() 為“局部奇函數”.若函數
為“局部奇函數”.若函數![]() 是定義在
是定義在![]() 上的“局部奇函數”,則實數
上的“局部奇函數”,則實數![]() 的取值范圍是( )
的取值范圍是( )
A. [1﹣![]() ,1+
,1+![]() ) B. [﹣1,2] C. [﹣2
) B. [﹣1,2] C. [﹣2![]() ,2
,2![]() ] D. [﹣2
] D. [﹣2![]() ,1﹣
,1﹣![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x|(x﹣a),a為實數.
(1)若函數f(x)為奇函數,求實數a的值;
(2)若函數f(x)在[0,2]為增函數,求實數a的取值范圍;
(3)是否存在實數a(a<0),使得f(x)在閉區間 ![]() 上的最大值為2,若存在,求出a的值;若不存在,請說明理由.
上的最大值為2,若存在,求出a的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=log3x.
(1)求f(45)﹣f(5)的值;
(2)若函數y=g(x)(x∈R)是奇函數,當x>0時,g(x)=f(x),求函數 y=g(x)的表達式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】記等差數列![]() 的前
的前![]() 項和為
項和為![]() .
.
(1)求證:數列![]() 是等差數列;
是等差數列;
(2)若 ![]() ,對任意
,對任意![]() ,均有
,均有![]() 是公差為
是公差為![]() 的等差數列,求使
的等差數列,求使![]() 為整數的正整數
為整數的正整數![]() 的取值集合;
的取值集合;
(3)記![]() ,求證:
,求證: ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com