Question

【題目】為了解高一學生暑假里在家讀書情況，特隨機調查了50名男生和50名女生平均每天的閱讀時間（單位：分鐘），統計如下表：

（1）根據統計表判斷男生和女生誰的平均讀書時間更長？并說明理由；

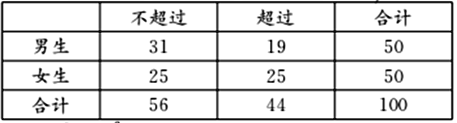
（2）求100名學生每天讀書時間的平均數，并將每天平均時間超過和不超過平均數的人數填入下列的列聯表：

（3）根據（2）中列聯表，能否有99%的把握認為“平均閱讀時間超過或不超過平均數是否與性別有關？”

附：

	0.050	0.010	0.001
	3.841	6.635	10.828

Answer 1

【答案】（1）見解析；（2）見解析；（3）見解析；

【解析】

（1）對表中數據的平均數，集中程度及中位數分析即可。

（2）計算出100名學生的平均讀書時間，對照表格求解即可

（3）由獨立性檢驗公式直接計算再判斷即可。

（1）女生平均每天讀書時間更長

理由如下：（i）分別求出男女生的平均讀書時間可知.

（ii）由統計表可估計，男生讀書時間的中位數大約為36.5分鐘，女生讀書時間的中位數大約是48.5分鐘，因此女生平均每天讀書時間更長.

（iii）由統計表可知，多數男生讀書時間主要集中在之間，而女生主要集中在之間，因此女生平均每天讀書時間更長..

（2）可求100名學生的平均讀書時間為：

，

列聯表如下：

（3）由于，

所以沒有99%的把握認為閱讀時間超過或不超過平均數與性別有關.