
【題目】已知函數(shù)![]() .
.
(1)若![]() 在
在![]() 單調(diào)遞增,求
單調(diào)遞增,求![]() 的值;
的值;
(2)當(dāng)![]() 時,設(shè)函數(shù)
時,設(shè)函數(shù)![]() 的最小值為
的最小值為![]() ,求函數(shù)
,求函數(shù)![]() 的值域.
的值域.
【答案】(1)![]() .(2)
.(2)![]()
【解析】
(1)對函數(shù)進(jìn)行求導(dǎo)得![]() ,由
,由![]() 在
在![]() 單調(diào)遞增,得
單調(diào)遞增,得![]() ,即
,即![]() ,利用分析法,對
,利用分析法,對![]() 進(jìn)行分類討論,即可得答案;
進(jìn)行分類討論,即可得答案;
(2)利用隱零點法求出函數(shù)![]() 最小值為
最小值為![]() ,得
,得![]() ,利用導(dǎo)數(shù)研究函數(shù)令
,利用導(dǎo)數(shù)研究函數(shù)令![]() ,的值域,即可得答案;
,的值域,即可得答案;
(1)![]() .
.
因為![]() 在
在![]() 單調(diào)遞增,所以
單調(diào)遞增,所以![]() ,即
,即![]()
(i)當(dāng)![]() 時,
時,![]() ,則需
,則需![]() ,故
,故![]() ,即
,即![]() ;
;
(ii)當(dāng)![]() 時,
時,![]() ,則
,則![]() ;
;
(iii)當(dāng)![]() 時,
時,![]() ,則需
,則需![]() ,故
,故![]() ,即
,即![]() .
.
綜上述,![]() .
.
(2)![]() .
.
因為![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 單調(diào)遞增
單調(diào)遞增
又因為![]() ,
,
所以存在![]() ,使
,使![]() ,
,
且當(dāng)![]() 時,
時,![]() ,函數(shù)
,函數(shù)![]() 單調(diào)遞減;
單調(diào)遞減;
當(dāng)![]() 時,
時,![]() ,函數(shù)
,函數(shù)![]() 單調(diào)遞增.
單調(diào)遞增.
故![]() 最小值為
最小值為![]() .
.
由![]() ,得
,得![]() ,因此
,因此![]() .
.
令![]() ,則
,則![]() ,
,
所以![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞增.
上單調(diào)遞增.
又因為![]() ,且
,且![]() ,
,
所以![]() ,即
,即![]() 取遍
取遍![]() 的每一個值,
的每一個值,
令![]() ,
,
則![]() ,
,
故函數(shù)![]() 在
在![]() 單調(diào)遞增.
單調(diào)遞增.
又![]() ,所以
,所以![]() ,故函數(shù)
,故函數(shù)![]() 的值域為
的值域為![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】某工廠為提高生產(chǎn)效率,需引進(jìn)一條新的生產(chǎn)線投入生產(chǎn),現(xiàn)有兩條生產(chǎn)線可供選擇,生產(chǎn)線①:有A,B兩道獨立運行的生產(chǎn)工序,且兩道工序出現(xiàn)故障的概率依次是0.02,0.03.若兩道工序都沒有出現(xiàn)故障,則生產(chǎn)成本為15萬元;若A工序出現(xiàn)故障,則生產(chǎn)成本增加2萬元;若B工序出現(xiàn)故障,則生產(chǎn)成本增加3萬元;若A,B兩道工序都出現(xiàn)故障,則生產(chǎn)成本增加5萬元.生產(chǎn)線②:有a,b兩道獨立運行的生產(chǎn)工序,且兩道工序出現(xiàn)故障的概率依次是0.04,0.01.若兩道工序都沒有出現(xiàn)故障,則生產(chǎn)成本為14萬元;若a工序出現(xiàn)故障,則生產(chǎn)成本增加8萬元;若b工序出現(xiàn)故障,則生產(chǎn)成本增加5萬元;若a,b兩道工序都出現(xiàn)故障,則生產(chǎn)成本增加13萬元.
(1)若選擇生產(chǎn)線①,求生產(chǎn)成本恰好為18萬元的概率;
(2)為最大限度節(jié)約生產(chǎn)成本,你會給工廠建議選擇哪條生產(chǎn)線?請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知角![]() 始邊與
始邊與![]() 軸的非負(fù)半軸重合,與圓
軸的非負(fù)半軸重合,與圓![]() 相交于點
相交于點![]() ,終邊與圓
,終邊與圓![]() 相交于點
相交于點![]() ,點
,點![]() 在
在![]() 軸上的射影為
軸上的射影為![]() ,
, ![]() 的面積為
的面積為![]() ,函數(shù)
,函數(shù)![]() 的圖象大致是( )
的圖象大致是( )
A. 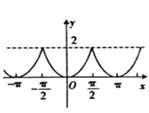 B.
B. 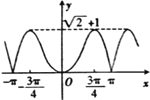
C. 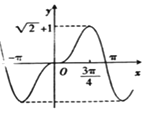 D.
D. 
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某外賣平臺為提高外賣配送效率,針對外賣配送業(yè)務(wù)提出了兩種新的配送方案,為比較兩種配送方案的效率,共選取50名外賣騎手,并將他們隨機(jī)分成兩組,每組25人,第一組騎手用甲配送方案,第二組騎手用乙配送方案.根據(jù)騎手在相同時間內(nèi)完成配送訂單的數(shù)量(單位:單)繪制了如下莖葉圖:
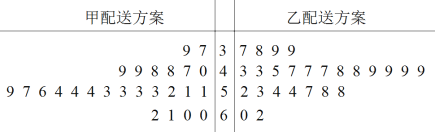
(1)根據(jù)莖葉圖,求各組內(nèi)25位騎手完成訂單數(shù)的中位數(shù),已知用甲配送方案的25位騎手完成訂單數(shù)的平均數(shù)為52,結(jié)合中位數(shù)與平均數(shù)判斷哪種配送方案的效率更高,并說明理由;
(2)設(shè)所有50名騎手在相同時間內(nèi)完成訂單數(shù)的平均數(shù)![]() ,將完成訂單數(shù)超過
,將完成訂單數(shù)超過![]() 記為“優(yōu)秀”,不超過
記為“優(yōu)秀”,不超過![]() 記為“一般”,然后將騎手的對應(yīng)人數(shù)填入下面列聯(lián)表;
記為“一般”,然后將騎手的對應(yīng)人數(shù)填入下面列聯(lián)表;
優(yōu)秀 | 一般 | |
甲配送方案 | ||
乙配送方案 |
(3)根據(jù)(2)中的列聯(lián)表,判斷能否有![]() 的把握認(rèn)為兩種配送方案的效率有差異.
的把握認(rèn)為兩種配送方案的效率有差異.
附: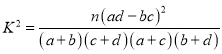 ,其中
,其中![]() .
.
| 0.05 | 0.010 | 0.005 |
| 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,已知曲線
中,已知曲線![]() :
: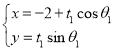 (
(![]() 為參數(shù)),曲線
為參數(shù)),曲線![]() :
: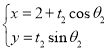 (
(![]() 為參數(shù)),且
為參數(shù)),且![]() ,點P為曲線
,點P為曲線![]() 與
與![]() 的公共點.
的公共點.
(1)求動點P的軌跡方程;
(2)在以原點O為極點,x軸的非負(fù)半軸為極軸的極坐標(biāo)系中,直線l的極坐標(biāo)方程為![]() ,求動點P到直線l的距離的取值范圍.
,求動點P到直線l的距離的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() 與圓
與圓![]() 相外切,且與直線
相外切,且與直線![]() 相切.
相切.
(1)記圓心![]() 的軌跡為曲線
的軌跡為曲線![]() ,求
,求![]() 的方程;
的方程;
(2)過點![]() 的兩條直線
的兩條直線![]() 與曲線
與曲線![]() 分別相交于點
分別相交于點![]() 和
和![]() ,線段
,線段![]() 和
和![]() 的中點分別為
的中點分別為![]() .如果直線
.如果直線![]() 與
與![]() 的斜率之積等于1,求證:直線
的斜率之積等于1,求證:直線![]() 經(jīng)過定點.
經(jīng)過定點.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() 是各項均為正數(shù)的等差數(shù)列,
是各項均為正數(shù)的等差數(shù)列,![]() ,
,![]() 是
是![]() 和
和![]() 的等比中項,
的等比中項,![]() 的前
的前![]() 項和為
項和為![]() ,
,![]() .
.
(1)求![]() 和
和![]() 的通項公式;
的通項公式;
(2)設(shè)數(shù)列![]() 的通項公式
的通項公式 .
.
(i)求數(shù)列![]() 的前
的前![]() 項和
項和![]() ;
;
(ii)求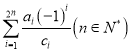 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】點![]() 與定點
與定點![]() 的距離和它到直線
的距離和它到直線![]() 的距離的比是常數(shù)
的距離的比是常數(shù)![]() .
.
(Ⅰ)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)過坐標(biāo)原點![]() 的直線交軌跡
的直線交軌跡![]() 于
于![]() ,
,![]() 兩點,軌跡
兩點,軌跡![]() 上異于
上異于![]() ,
,![]() 的點
的點![]() 滿足直線
滿足直線![]() 的斜率為
的斜率為![]() .
.
(ⅰ)證明:直線![]() 與
與![]() 的斜率之積為定值;
的斜率之積為定值;
(ⅱ)求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為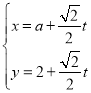 (
(![]() 為參數(shù)),以坐標(biāo)原點
為參數(shù)),以坐標(biāo)原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標(biāo)系,曲線
軸正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求直線![]() 和曲線
和曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)若點![]() 坐標(biāo)為
坐標(biāo)為![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,且
兩點,且![]() ,求實數(shù)
,求實數(shù)![]() 的值.
的值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com