
【題目】設橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,右頂點為
,右頂點為![]() ,上頂點為
,上頂點為![]() ,已知
,已知![]() .
.
(1)求橢圓的離心率;
(2)設![]() 為橢圓上異于其頂點的一點,以線段
為橢圓上異于其頂點的一點,以線段![]() 為直徑的圓經過點
為直徑的圓經過點![]() ,經過原點
,經過原點![]() 的直線
的直線![]() 與該圓相切,求直線
與該圓相切,求直線![]() 的斜率.
的斜率.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
試題分析:(1)設橢圓右焦點![]() 的坐標為
的坐標為![]() ,由
,由![]() ,可得
,可得![]() ,又
,又![]() ,即可求解橢圓的離心率;(2)由(1)知
,即可求解橢圓的離心率;(2)由(1)知![]() ,得到橢圓的方程為
,得到橢圓的方程為![]() ,設出點
,設出點![]() ,可得
,可得![]() ,進而得到
,進而得到![]() ,由于點
,由于點![]() 在橢圓上,聯立得到
在橢圓上,聯立得到![]() ,解得
,解得![]() ,利用中點公式和兩點間的距離公式,利用直線與圓相切的性質即可得出結論.
,利用中點公式和兩點間的距離公式,利用直線與圓相切的性質即可得出結論.
試題解析:(1)設橢圓右焦點![]() 的坐標為
的坐標為![]() ,由
,由![]() ,可得
,可得![]() .
.
又![]() ,則
,則![]() ,所以橢圓的離心率
,所以橢圓的離心率![]() .
.
(2)由(1)知![]() ,故橢圓的方程為
,故橢圓的方程為![]() ,
,
設![]() ,由
,由![]() ,有
,有![]() ,
,
由已知,有![]() ,即
,即![]() ,又
,又![]() ,故有
,故有![]() . ①
. ①
又因為點![]() 在橢圓上,所以
在橢圓上,所以![]() .②
.②
由 ①和②可得![]() ,而點
,而點![]() 不是橢圓的頂點,故
不是橢圓的頂點,故![]() ,
,
代人①得![]() ,即點
,即點![]() 的坐標為
的坐標為![]() ,設圓的圓心為
,設圓的圓心為![]() ,
,
則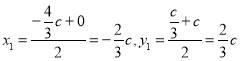 ,進而圓的半徑
,進而圓的半徑![]() ,
,
設直線![]() 的斜率為
的斜率為![]() ,依題意,直線
,依題意,直線![]() 的方程
的方程![]() .由
.由![]() 與圓相切,可得
與圓相切,可得![]() ,
,
即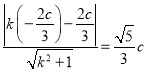 ,整理得
,整理得![]() ,解得
,解得![]() ,
,
所以直線![]() 的斜率為
的斜率為![]() 或
或![]() .
.


科目:高中數學 來源: 題型:
【題目】選修4—4:坐標系與參數方程
已知平面直角坐標系![]() ,以
,以![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,
軸的非負半軸為極軸建立極坐標系,![]() 點的極坐標為
點的極坐標為![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為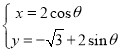 (
(![]() 為參數).
為參數).
(1)寫出點![]() 的直角坐標及曲線
的直角坐標及曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 為曲線
為曲線![]() 上的動點,求
上的動點,求![]() 中點
中點![]() 到直線
到直線![]() 的距離的最小值.
的距離的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了保護環境,2015年合肥市勝利工廠在市政府的大力支持下,進行技術改進:把二氧化碳轉化為某種化工產品,經測算,該處理成本![]() (萬元)與處理量
(萬元)與處理量![]() (噸)之間的函數關系可近似地表示為:
(噸)之間的函數關系可近似地表示為: 且每處理一噸二氧化碳可得價值為20萬元的某種化工產品.
且每處理一噸二氧化碳可得價值為20萬元的某種化工產品.
(1)當![]() 時,判斷該技術改進能否獲利?如果能獲利,求出最大利潤;如果不能獲利,則國家至少需要補貼多少萬元,該工廠才不虧損?
時,判斷該技術改進能否獲利?如果能獲利,求出最大利潤;如果不能獲利,則國家至少需要補貼多少萬元,該工廠才不虧損?
(2)當處理量為多少噸時,每噸的平均處理成本最少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,離心率為
,離心率為![]() ,點
,點![]() 為坐標原點,若橢圓
為坐標原點,若橢圓![]() 與曲線
與曲線![]() 的交點分別為
的交點分別為![]() (
(![]() 下
下![]() 上),且
上),且![]() 兩點滿足
兩點滿足![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過橢圓![]() 上異于其頂點的任一點
上異于其頂點的任一點![]() ,作
,作![]() 的兩條切線,切點分別為
的兩條切線,切點分別為![]() ,且直線
,且直線![]() 在
在![]() 軸、
軸、![]() 軸上的截距分別為
軸上的截距分別為![]() ,證明:
,證明:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市有一直角梯形綠地![]() ,其中
,其中![]() ,
,![]() km,
km,![]() km.現過邊界
km.現過邊界![]() 上的點
上的點![]() 處鋪設一條直的灌溉水管
處鋪設一條直的灌溉水管![]() ,將綠地分成面積相等的兩部分.
,將綠地分成面積相等的兩部分.
(1)如圖①,若![]() 為
為![]() 的中點,
的中點,![]() 在邊界
在邊界![]() 上,求灌溉水管
上,求灌溉水管![]() 的長度;
的長度;
(2)如圖②,若![]() 在邊界
在邊界![]() 上,求灌溉水管
上,求灌溉水管![]() 的最短長度.
的最短長度.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了在冬季供暖時減少能量損耗,房屋的屋頂和外墻需要建造隔熱層,某幢建筑物要建造可使用20年的隔熱層,每厘米厚的隔熱層建造成本為6萬元,該建筑物每年的能源消耗費用![]() (單位:萬元)與隔熱層厚度
(單位:萬元)與隔熱層厚度![]() (單位:
(單位:![]() )滿足關系:
)滿足關系:![]() ,若不建隔熱層,每年能源消耗費用為8萬元,設
,若不建隔熱層,每年能源消耗費用為8萬元,設![]() 為隔熱層建造費用與20年的能源消耗費用之和.
為隔熱層建造費用與20年的能源消耗費用之和.
(1)求![]() 的值及
的值及![]() 的表達式;
的表達式;
(2)隔熱層修建多厚時,總費用![]() 達到最小,并求最小值.
達到最小,并求最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位每天的用電量![]() (度)與當天最高氣溫
(度)與當天最高氣溫![]() (℃)之間具有線性相關關系,下表是該單位隨機統計4天的用電量與當天最高氣溫的數據.
(℃)之間具有線性相關關系,下表是該單位隨機統計4天的用電量與當天最高氣溫的數據.
最高氣溫(℃) | 26 | 29 | 31 | 34 |
用電量 (度) | 22 | 26 | 34 | 38 |
(Ⅰ)根據表中數據,求出回歸直線的方程![]() (其中
(其中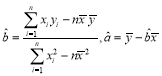 );
);
(Ⅱ)試預測某天最高氣溫為33℃時,該單位當天的用電量(精確到1度).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com