
【題目】已知四棱錐![]() 的五個頂點都在球O的球面上,
的五個頂點都在球O的球面上,![]() ,
,![]() ,
,![]() ,
,![]() 是等邊三角形,若四棱錐
是等邊三角形,若四棱錐![]() 體積的最大值
體積的最大值![]() ,則球O的表面積為( )
,則球O的表面積為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,點
,點![]() 是橢圓
是橢圓![]() 上的點.
上的點.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)已知斜率存在又不經過原點的直線![]() 與圓
與圓![]() 相切,且與橢圓
相切,且與橢圓![]() 交于
交于![]() 兩點.探究:在橢圓
兩點.探究:在橢圓![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() ,若存在,請求出實數
,若存在,請求出實數![]() 的取值范圍,若不存在,請說明理由.
的取值范圍,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中石化集團通過與安哥拉國家石油公司合作,獲得了安哥拉深海油田區塊的開采權,集團在某些區塊隨機初步勘探了部分舊井,取得了地質資料.進入全面勘探時期后集團按網絡點來布置井位來進行全面勘探.由于勘探一口井的費用很高,如果新設計的井位與原有井位重合或接近,便利用舊井的地質資料,不必打這口新井,以節約勘探費用.勘探初期數據資料見下表:
井位 | 1 | 2 | 3 | 4 | 5 | 6 |
坐標 |
|
|
|
|
|
|
鉆探深度 | 2 | 4 | 5 | 6 | 8 | 10 |
出油量 | 40 | 70 | 110 | 90 | 160 | 205 |
(1)若1![]() 6號舊井位置滿足線性分布,借助前5組數據所求得的回歸直線方程為
6號舊井位置滿足線性分布,借助前5組數據所求得的回歸直線方程為![]() ,且
,且![]() ,求
,求![]() ,并估計
,并估計![]() 的預報值;
的預報值;
(2)現準備勘探新井7(1,25),若通過,1,3,5,7號井計算出的![]() ,
,![]() 的值與(1)中
的值與(1)中![]() ,
,![]() 的值的差不超過10%,則使用位置最接近的舊井
的值的差不超過10%,則使用位置最接近的舊井![]() ,否則在新位置打井,請判斷可否使用舊井?(注:其中
,否則在新位置打井,請判斷可否使用舊井?(注:其中![]() 的計算結果用四舍五入法保留一位小數)
的計算結果用四舍五入法保留一位小數)
參考數據:![]()
參考公式:
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有甲乙丙丁四個人相互之間傳球,從甲開始傳球,甲等可能地把球傳給乙丙丁中的任何一個人,依此類推.
(1)通過三次傳球后,球經過乙的次數為ξ,求ξ的分布列和期望;
(2)設經過n次傳球后,球落在甲手上的概率為an,
(i)求a1,a2,an;
(ii)探究:隨著傳球的次數足夠多,球落在甲乙丙丁每個人手上的概率是否相等,并簡單說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,圓O是一半徑為10米的圓形草坪,為了滿足周邊市民跳廣場舞的需要,現規劃在草坪上建一個廣場,廣場形狀如圖中虛線部分所示的曲邊四邊形,其中A,B兩點在⊙O上,A,B,C,D恰是一個正方形的四個頂點.根據規劃要求,在A,B,C,D四點處安裝四盞照明設備,從圓心O點出發,在地下鋪設4條到A,B,C,D四點線路OA,OB,OC,OD.
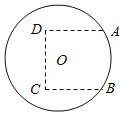
(1)若正方形邊長為10米,求廣場的面積;
(2)求鋪設的4條線路OA,OB,OC,OD總長度的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線C:![]() (a>0,b>0)的左、右焦點分別為F1,F2,P為雙曲線C上的一點,線段PF1與y軸的交點M恰好是線段PF1的中點,
(a>0,b>0)的左、右焦點分別為F1,F2,P為雙曲線C上的一點,線段PF1與y軸的交點M恰好是線段PF1的中點,![]() ,其中O為坐標原點,則雙曲線C的漸近線的斜率與離心率分別是( )
,其中O為坐標原點,則雙曲線C的漸近線的斜率與離心率分別是( )
A. ±1,![]() B. 1,
B. 1,![]() C. ±2,
C. ±2,![]() D. 2,
D. 2,![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com