
已知數列 滿足
滿足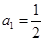 ,
,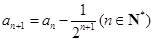 .
.
(1)求數列 的通項公式;
的通項公式;
(2)令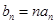 ,數列{bn}的前n項和為Tn,試比較Tn與
,數列{bn}的前n項和為Tn,試比較Tn與 的大小,并予以證明.
的大小,并予以證明.
(1) ;(2)詳見解析.
;(2)詳見解析.
解析試題分析:(1)由于數列 的遞推式的結構為
的遞推式的結構為 ,在求數列的通項的時候可以利用累加法來求數列
,在求數列的通項的時候可以利用累加法來求數列 的通項公式;(2)先求出數列
的通項公式;(2)先求出數列 的通項公式,根據其通項結構選擇錯位相減法求出數列
的通項公式,根據其通項結構選擇錯位相減法求出數列 的前
的前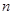 項和
項和 ,在比較
,在比較 與
與 的大小時,一般利用作差法,通過差的正負確定
的大小時,一般利用作差法,通過差的正負確定 與
與 的大小,在確定差的正負時,可以利用數學歸納法結合二項式定理進行放縮來達到證明不等式的目的.
的大小,在確定差的正負時,可以利用數學歸納法結合二項式定理進行放縮來達到證明不等式的目的.
試題解析:(1)當 時,
時,


 .
.
又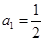 也適合上式,所以
也適合上式,所以 .
.
(2)由(1)得 ,所以
,所以 .
.
因為 ①,所以
①,所以 ②.
②.
由①-②得, ,
,
所以 .
.
因為 ,
,
所以確定 與
與 的大小關系等價于比較
的大小關系等價于比較 與
與 的大小.
的大小.
當 時,
時, ;當
;當 時,
時, ;
;
當 時,
時, ;當
;當 時,
時, ;……,
;……,
可猜想當 時,
時, .
.
證明如下:當 時,
時,
 .
.
綜上所述,當 或
或 時,
時, ;當
;當 時,
時, .
.
考點:累加法、錯位相減法、二項式定理


 同步輕松練習系列答案
同步輕松練習系列答案 課課通課程標準思維方法與能力訓練系列答案
課課通課程標準思維方法與能力訓練系列答案科目:高中數學 來源: 題型:解答題
設數列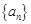 的前
的前 項和為
項和為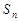 ,若對任意
,若對任意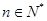 ,都有
,都有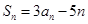 .
.
⑴求數列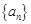 的首項;
的首項;
⑵求證:數列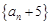 是等比數列,并求數列
是等比數列,并求數列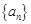 的通項公式;
的通項公式;
⑶數列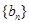 滿足
滿足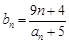 ,問是否存在
,問是否存在 ,使得
,使得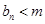 恒成立?如果存在,求出
恒成立?如果存在,求出 的值,如果不存在,說明理由.
的值,如果不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com