
【題目】某公司生產一種電子儀器的固定成本為20000元,每生產一臺儀器需增加投入100元,已知總收益滿足函數:  ,其中
,其中![]() 是儀器的月產量.(注:總收益=總成本+利潤)
是儀器的月產量.(注:總收益=總成本+利潤)
(1)將利潤![]() 表示為月產量
表示為月產量![]() 的函數;
的函數;
(2)當月產量為何值時,公司所獲利潤最大?最大利潤為多少元?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】如圖,設橢圓 ![]() +
+ ![]() =1(a>b>0)的左右焦點分別為F1 , F2 , 點D在橢圓上,DF1⊥F1F2 ,
=1(a>b>0)的左右焦點分別為F1 , F2 , 點D在橢圓上,DF1⊥F1F2 , ![]() =2
=2 ![]() ,△DF1F2的面積為
,△DF1F2的面積為 ![]() . (Ⅰ)求該橢圓的標準方程;
. (Ⅰ)求該橢圓的標準方程;
(Ⅱ)是否存在圓心在y軸上的圓,使圓在x軸的上方與橢圓有兩個交點,且圓在這兩個交點處的兩條切線互相垂直并分別過不同的焦點?若存在,求出圓的方程;若不存在,請說明理由.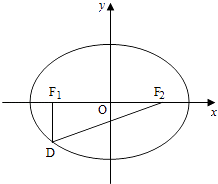
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=(x2﹣2ax)lnx+2ax﹣ ![]() x2 , 其中a∈R.
x2 , 其中a∈R.
(1)若a=0,且曲線f(x)在x=t處的切線l過原點,求直線l的方程;
(2)求f(x)的極值;
(3)若函數f(x)有兩個極值點x1 , x2(x1<x2),證明f(x1)+f(x2)< ![]() a2+3a.
a2+3a.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法錯誤的是( )
A. 在殘差圖中,殘差點分布的帶狀區域的寬度越狹窄,其模型擬合的精度越高
B. 在線性回歸分析中,回歸直線不一定過樣本點的中心![]()
C. 在回歸分析中, ![]() 為0.98的模型比
為0.98的模型比![]() 為0.80的模型擬合的效果好
為0.80的模型擬合的效果好
D. 自變量取值一定時,因變量的取值帶有一定隨機性的兩個變量之間的關系叫做相關關系
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有甲、乙兩個盒子,甲盒子中有8張卡片,其中2張寫有數字0,3張寫有數字1,3張寫有數字2;乙盒子中有8張卡片,其中3張寫有數字0,2張寫有數字1,3張寫有數字2.
(1)如果從甲盒子中取2張卡片,從乙盒中取1張卡片,那么取出的3張卡片都寫有1的概率是多少?
(2)如果從甲、乙兩個盒子中各取1張卡片,設取出的兩張卡片數字之和為X,求X的概率分布.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的內角A、B、C的對邊分別為a、b、c,且3bcos A=ccos A+acosC.
(1)求tanA的值;
(2)若a=4 ![]() ,求△ABC的面積的最大值.
,求△ABC的面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com