
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,橢圓
,橢圓![]() 和拋物線
和拋物線![]() 交于
交于![]() 兩點,且直線
兩點,且直線![]() 恰好通過橢圓
恰好通過橢圓![]() 的右焦點.
的右焦點.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)經過橢圓![]() 右焦點的直線
右焦點的直線![]() 和橢圓
和橢圓![]() 交于
交于![]() 兩點,點
兩點,點![]() 在橢圓上,且
在橢圓上,且![]() ,
,
其中![]() 為坐標原點,求直線
為坐標原點,求直線![]() 的斜率.
的斜率.
科目:高中數學 來源: 題型:
【題目】為響應國家“精準扶貧,產業扶貧“的戰略,進一步優化能源消費結構,某市決定在一地處山區的![]() 縣推進光伏發電項目,在該縣山區居民中隨機抽取50戶,統計其年用電量得到以下統計表,以樣本的頻率作為概率.
縣推進光伏發電項目,在該縣山區居民中隨機抽取50戶,統計其年用電量得到以下統計表,以樣本的頻率作為概率.
用電量(度) |
|
|
|
|
|
戶數 | 5 | 15 | 10 | 15 | 5 |
(1)在該縣山區居民中隨機抽取10戶,記其中年用電量不超過600度的戶數為![]() ,求
,求![]() 的數學期望;
的數學期望;
(2)已知該縣某山區自然村有居民300戶,若計劃在該村安裝總裝機容量為300千瓦的光伏發電機組,該機組所發電量除保證該村正常用電外,剩余電量國家電網以![]() 元/度進行收購.經測算以每千瓦裝機容量平均發電1000度,試估計該機組每年所發電量除保證正常用電外還能為該村創造直接收益多少元?
元/度進行收購.經測算以每千瓦裝機容量平均發電1000度,試估計該機組每年所發電量除保證正常用電外還能為該村創造直接收益多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱錐![]() 中,
中, ![]() 和
和![]() 是邊長為
是邊長為![]() 的等邊三角形,
的等邊三角形, ![]() ,
, ![]() 是
是![]() 中點,
中點, ![]() 是
是![]() 中點.
中點.
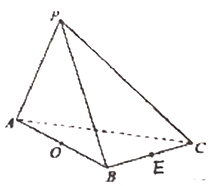
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)求直線![]() 與平面
與平面![]() 所成角的正弦值的大小;
所成角的正弦值的大小;
(Ⅲ)在棱![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 的余弦值為
的余弦值為![]() ?若存在,指出點
?若存在,指出點![]() 在
在![]() 上的位置;若不存在,說明理由.
上的位置;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位從一所學校招收某類特殊人才,對20位已經選拔入圍的學生進行運動協調能力和邏輯思維能力的測試,其測試結果如下表:
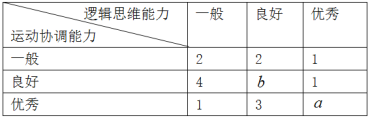
例如表中運動協調能力良好且邏輯思維能力一般的學生是4人,由于部分數據丟失,只知道從這20位參加測試的學生中隨機抽取一位,抽到邏輯思維能力優秀的學生的概率為![]() .
.
(1)求![]() 、
、![]() 的值;
的值;
(2)從運動協調能力為優秀的學生中任意抽取2位,求其中至少有一位邏輯思維能力優秀的學生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】交強險是車主必須為機動車購買的險種,若普通![]() 座以下私家車投保交強險第一年的費用(基準保費)統一為
座以下私家車投保交強險第一年的費用(基準保費)統一為![]() 元,在下一年續保時,實行的是費率浮動機制,保費與上一年度車輛發生道路交通事故的情況相聯系,發生交通事故的次數越多,費率也就越高,具體浮動情況如下表:
元,在下一年續保時,實行的是費率浮動機制,保費與上一年度車輛發生道路交通事故的情況相聯系,發生交通事故的次數越多,費率也就越高,具體浮動情況如下表:

某機構為了研究某一品牌普通![]() 座以下私家車的投保情況,隨機抽取了
座以下私家車的投保情況,隨機抽取了![]() 輛車齡已滿三年的該品牌同型號私家車的下一年續保時的情況,統計得到了下面的表格:
輛車齡已滿三年的該品牌同型號私家車的下一年續保時的情況,統計得到了下面的表格:
類型 |
|
|
|
|
|
|
數量 | 10 | 5 | 5 | 20 | 15 | 5 |
以這![]() 輛該品牌車的投保類型的頻率代替一輛車投保類型的概率,完成下列問題:
輛該品牌車的投保類型的頻率代替一輛車投保類型的概率,完成下列問題:
(Ⅰ)按照我國《機動車交通事故責任強制保險條例》汽車交強險價格的規定, ![]() ,記
,記![]() 為某同學家里的一輛該品牌車在第四年續保時的費用,求
為某同學家里的一輛該品牌車在第四年續保時的費用,求![]() 的分布列與數學期望;(數學期望值保留到個位數字)
的分布列與數學期望;(數學期望值保留到個位數字)
(Ⅱ)某二手車銷售商專門銷售這一品牌的二手車,且將下一年的交強險保費高于基本保費的車輛記為事故車,假設購進一輛事故車虧損![]() 元,一輛非事故車盈利
元,一輛非事故車盈利![]() 元:
元:
①若該銷售商購進三輛(車齡已滿三年)該品牌二手車,求這三輛車中至少有一輛事故車的概率;
②若該銷售商一次購進![]() 輛(車齡已滿三年)該品牌二手車,求他獲得利潤的期望值.
輛(車齡已滿三年)該品牌二手車,求他獲得利潤的期望值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]()
若![]() ,過點
,過點![]() 的直線
的直線![]() 交曲線
交曲線![]() 于
于![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的方程;
的方程;
若曲線![]() 表示圓,且直線
表示圓,且直線![]() 與圓
與圓![]() 交于
交于![]() 兩點,是否存在實數
兩點,是否存在實數![]() ,使得以
,使得以![]() 為直徑的圓過原點,若存在,求出實數
為直徑的圓過原點,若存在,求出實數![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,圓
中,圓![]() 的參數方程
的參數方程![]() ,以
,以![]() 為極點,
為極點, ![]() 軸的非負半軸為極軸建立極坐標系.
軸的非負半軸為極軸建立極坐標系.
(Ⅰ)求圓![]() 的極坐標方程;
的極坐標方程;
(Ⅱ)直線![]() 的極坐標方程是
的極坐標方程是![]() ,射線
,射線![]() 與圓
與圓![]() 的交點為
的交點為![]() ,與直線
,與直線![]() 的交點為
的交點為![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com