已知函數f(x)=ex,直線l的方程為y=kx+b.
(1)求過函數圖象上的任一點P(t,f(t))的切線方程;
(2)若直線l是曲線y=f(x)的切線,求證:f(x)≥kx+b對任意x∈R成立;
(3)若f(x)≥kx+b對任意x∈[0,+∞)成立,求實數k、b應滿足的條件.
【答案】
分析:(1)對函數求導,得到函數的導函數,即得到了函數在某一點的切線的斜率,用點斜式寫出切線的方程.
(2)根據切線的方程,寫出斜率和截距,構造新函數,對新函數求導,得到在x∈(-∞,t)上單調遞減,在x∈(t,+∞)為單調遞增,即得到函數的最小值,根據函數思想得到不等式成立.
(3)構造新函數,對新函數求導,判斷函數的單調性,針對于k的不同值,函數的單調性不同,需要進行討論,求出函數的最小值,得到要寫的條件.
解答:解:(1)函數f(x)=e
x,
分析可得f(x)=e
x與直線相切,只有一個交點即切點,
故過函數圖象上的任一點P(t,f(t))的切線中P即為切點,
∵f'(x)=e
x,
∴切線l的方程為y-e
t=e
t(x-t)
即y=e
tx+e
t(1-t)
(2)由(1)

記函數F(x)=f(x)-kx-b,
∴F(x)=e
x-e
tx-e
t(1-t)
∴F'(x)=e
x-e
t∴F(x)在x∈(-∞,t)上單調遞減,在x∈(t,+∞)為單調遞增
故F(x)
min=F(t)=e
t-e
tt-e
t(1-t)=0
故F(x)=f(x)-kx-b≥0即f(x)≥kx+b對任意x∈R成立
(3)設H(x)=f(x)-kx-b=e
x-kx-b,x∈[0,+∞)
∴H'(x)=e
x-k,x∈[0,+∞)
①當k≤1時,H'(x)≥0,則H(x)在x∈[0,+∞)上單調遞增
∴H(x)
min=H(0)=1-b≥0,
∴b≤1,即
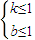
符合題意
②當k>1時,H(x)在x∈[0,lnk)上單調遞減,x∈[lnk,+∞)上單調遞增
∴H(x)
min=H(lnk)=k-klnk-b≥0
∴b≤k(1-lnk)
綜上所述滿足題意的條件是
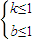
或
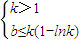 點評:
點評:本題考查函數導函數的應用,主要是求最值問題,本題解題的關鍵是對于不等式成立,只要用函數的最值來整理就使得問題解題的方向非常明確.


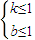 符合題意
符合題意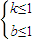 或
或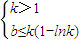


 名校課堂系列答案
名校課堂系列答案