
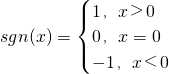 ,若已知函數
,若已知函數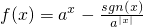 (a>0且a≠1)滿足f(1)=
(a>0且a≠1)滿足f(1)= .
. =
= ,∴a=2或-
,∴a=2或- (舍),…(1分)
(舍),…(1分) ≥2,∵f(x)=
≥2,∵f(x)= ≤2,∴
≤2,∴ =2,∴
=2,∴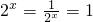 ,∴x=0;
,∴x=0;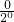 =1≤2,∴x=0,…(4分)
=1≤2,∴x=0,…(4分)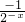 =2x+1≤2,∴x≤0,
=2x+1≤2,∴x≤0,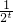 ,f(2t)=22t+
,f(2t)=22t+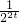 ,
,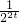 +m(2t+
+m(2t+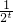 )+4≥0恒成立,…(8分)
)+4≥0恒成立,…(8分)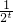 (t>0)∈[2,+∞),…(9分)
(t>0)∈[2,+∞),…(9分)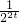 +m(2t+
+m(2t+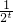 )+4=u2-2+mu+4=u2+mu+2≥0恒成立,
)+4=u2-2+mu+4=u2+mu+2≥0恒成立,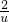 )(u∈[2,+∞))恒成立,
)(u∈[2,+∞))恒成立,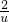 )]max(u∈[2,+∞)),…(11分)
)]max(u∈[2,+∞)),…(11分)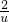 )在[2,+∞)上單調遞減,…(12分)
)在[2,+∞)上單調遞減,…(12分)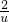 )]max(u∈[2,+∞))=-3,…(13分)
)]max(u∈[2,+∞))=-3,…(13分) ,可求a的值,根據所給定義,分類討論化簡函數,分別解不等式,即可得到結論;
,可求a的值,根據所給定義,分類討論化簡函數,分別解不等式,即可得到結論;

科目:高中數學 來源: 題型:
| 3 |
| x |
| 3 |
| t |
| x |
| t |
| t |
| 4x2-12x-3 |
| 2x+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
|
| sgn(x) |
| a|x| |
| 3 |
| 2 |
查看答案和解析>>
科目:高中數學 來源:2011-2012學年上海浦東高三第六次聯考理科數學 題型:解答題
(本題共2小題,滿分14分。第1小題滿分7分,第2小題滿分7分)
定義: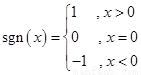 ,若已知函數
,若已知函數 (
(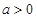 且
且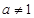 )滿足
)滿足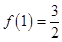 .
.
(1)解不等式: ;
;
(2)若 對于任意正實數
對于任意正實數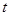 恒成立,求實數
恒成立,求實數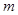 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com