
【題目】已知點A(0,﹣2),橢圓E: ![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ![]() ,F是橢圓的焦點,直線AF的斜率為
,F是橢圓的焦點,直線AF的斜率為 ![]() ,O為坐標原點.
,O為坐標原點.
(Ⅰ)求E的方程;
(Ⅱ)設過點A的直線l與E相交于P,Q兩點,當△OPQ的面積最大時,求l的方程.
【答案】解:(Ⅰ) 設F(c,0),由條件知 ![]() ,得
,得 ![]() 又
又 ![]() ,
,
所以a=2,b2=a2﹣c2=1,故E的方程 ![]() .
.
(Ⅱ)依題意當l⊥x軸不合題意,故設直線l:y=kx﹣2,設P(x1 , y1),Q(x2 , y2)
將y=kx﹣2代入 ![]() ,得(1+4k2)x2﹣16kx+12=0,
,得(1+4k2)x2﹣16kx+12=0,
當△=16(4k2﹣3)>0,即 ![]() 時,
時, ![]()
從而 ![]()
又點O到直線PQ的距離 ![]() ,所以△OPQ的面積
,所以△OPQ的面積 ![]() =
= ![]() ,
,
設 ![]() ,則t>0,
,則t>0, 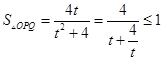 ,
,
當且僅當t=2,k=± ![]() 等號成立,且滿足△>0,
等號成立,且滿足△>0,
所以當△OPQ的面積最大時,l的方程為:y= ![]() x﹣2或y=﹣
x﹣2或y=﹣ ![]() x﹣2
x﹣2
【解析】(Ⅰ)通過離心率得到a、c關系,通過A求出a,即可求E的方程;(Ⅱ)設直線l:y=kx﹣2,設P(x1 , y1),Q(x2 , y2)將y=kx﹣2代入 ![]() ,利用△>0,求出k的范圍,利用弦長公式求出|PQ|,然后求出△OPQ的面積表達式,利用換元法以及基本不等式求出最值,然后求解直線方程.
,利用△>0,求出k的范圍,利用弦長公式求出|PQ|,然后求出△OPQ的面積表達式,利用換元法以及基本不等式求出最值,然后求解直線方程.


 全能測控一本好卷系列答案
全能測控一本好卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐![]() ,底面
,底面![]() 為菱形,
為菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 分別是
分別是![]() 的中點.
的中點.
(Ⅰ)證明: ![]() ;
;
(Ⅱ)若![]() 為
為![]() 上的動點,
上的動點, ![]() 與平面
與平面![]() 所成最大角的正切值為
所成最大角的正切值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】由于被墨水污染,一道數學題僅能見到如下文字:“已知二次函數![]() 的圖像經過
的圖像經過![]() ,
,![]() ,求證:這個二次函數的圖像關于直線
,求證:這個二次函數的圖像關于直線![]() 對稱”,根據已知消息,題中二次函數圖像不具有的性質是( ).
對稱”,根據已知消息,題中二次函數圖像不具有的性質是( ).
A. 在![]() 軸上的截線段長是
軸上的截線段長是![]() B. 與
B. 與![]() 軸交于點
軸交于點![]()
C. 頂點![]() D. 過點
D. 過點![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數![]() ,若
,若![]() ,則稱
,則稱![]() 為
為![]() 的“不動點”;若
的“不動點”;若![]() ,則稱
,則稱![]() 為
為![]() 的“穩定點”.函數
的“穩定點”.函數![]() 的“不動點”和“穩定點”的集合分別記為
的“不動點”和“穩定點”的集合分別記為![]() 和
和![]() ,即
,即![]() ,
,![]() .
.
(![]() )設函數
)設函數![]() ,求集合
,求集合![]() 和
和![]() .
.
(![]() )求證:
)求證:![]() .
.
(![]() )設函數
)設函數![]() ,且
,且![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有一個公益廣告說:“若不注意節約用水,那么若干年后,最有一滴水只能是我們的眼淚。”我國是水資源匱乏的國家。為鼓勵節約用水,某市打算出臺一項水費政策措施,規定:每一季度每人用水量不超過5噸時,每噸水費收基本價1.3元;若超過5噸而不超過6噸時,超過部分的水費加收200%;若超過6噸而不超過7噸時,超過部分的水費加收400%。設某人本季度實際用水量為![]() 噸,應交水費為f(x),(1)求
噸,應交水費為f(x),(1)求![]() 的值;(2)試求出函數f(x)的解析式。
的值;(2)試求出函數f(x)的解析式。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() 是
是![]() 上一點.
上一點.
(1)求橢圓![]() 的方程;
的方程;
(2)設![]() 是
是![]() 分別關于兩坐標軸及坐標原點的對稱點,平行于
分別關于兩坐標軸及坐標原點的對稱點,平行于![]() 的直線
的直線![]() 交
交![]() 于異于
于異于![]() 的兩點
的兩點![]() .點
.點![]() 關于原點的對稱點為
關于原點的對稱點為![]() .證明:直線
.證明:直線![]() 與
與![]() 軸圍成的三角形是等腰三角形.
軸圍成的三角形是等腰三角形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com