
【題目】設函數![]() .
.
(1)討論函數![]() 的單調性;
的單調性;
(2)如果對所有的![]() ≥1,都有
≥1,都有![]() ≤
≤![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)函數![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 單調遞增;(Ⅱ)
單調遞增;(Ⅱ)![]() .
.
【解析】
試題(Ⅰ)先對函數![]() 求導,再對
求導,再對![]() 的取值范圍進行討論,即可得
的取值范圍進行討論,即可得![]() 的單調性;(Ⅱ)設
的單調性;(Ⅱ)設![]() ,先對函數
,先對函數![]() 求導,再對
求導,再對![]() 的取值范圍進行討論函數
的取值范圍進行討論函數![]() 的單調性,進而可得
的單調性,進而可得![]() 的取值范圍.
的取值范圍.
試題解析:(Ⅰ)![]() 的定義域為
的定義域為![]() ,
,![]() 2分
2分
當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() 3分
3分
所以函數![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 單調遞增. 5分
單調遞增. 5分
(Ⅱ)法一:設![]() ,則
,則![]()
因為![]() ≥1,所以
≥1,所以![]() 7分
7分
(ⅰ)當![]() 時,
時,![]() ,
,![]() ,所以
,所以![]() 在
在![]() 單調遞減,而
單調遞減,而![]() ,所以對所有的
,所以對所有的![]() ≥1,
≥1,![]() ≤0,即
≤0,即![]() ≤
≤![]() ;
;
(ⅱ)當![]() 時,
時,![]() ,若
,若![]() ,則
,則![]() ,
,![]() 單調遞增,而
單調遞增,而![]() ,所以當
,所以當![]() 時,
時,![]() ,即
,即![]() ;
;
(ⅲ)當![]() 時,
時,![]() ,
,![]() ,所以
,所以![]() 在
在![]() 單調遞增,而
單調遞增,而![]() ,所以對所有的
,所以對所有的![]() ≥1,
≥1,![]() ,即
,即![]() ;
;
綜上,![]() 的取值范圍是
的取值范圍是![]() 12分
12分
法二:當![]() ≥1時,
≥1時,![]() ≤
≤![]()
![]() 6分
6分
令![]() ,則
,則![]() 7分
7分
令![]() ,則
,則![]() ,當
,當![]() ≥1時,
≥1時,![]() 8分
8分
于是![]() 在
在![]() 上為減函數,從而
上為減函數,從而![]() ,因此
,因此![]() , 9分
, 9分
于是![]() 在
在![]() 上為減函數,所以當
上為減函數,所以當![]() 時
時![]() 有最大值
有最大值![]() , 11分
, 11分
故![]() ,即
,即![]() 的取值范圍是
的取值范圍是![]() . 12分
. 12分


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某學校為倡導全體學生為特困學生捐款,舉行“一元錢,一片心,誠信用水”活動,學生在購水處每領取一瓶礦泉水,便自覺向捐款箱中至少投入一元錢。現統計了連續5天的售出和收益情況,如下表:
售出水量x(單位:箱) | 7 | 6 | 6 | 5 | 6 |
收益y(單位:元) | 165 | 142 | 148 | 125 | 150 |
(Ⅰ) 若x與y成線性相關,則某天售出8箱水時,預計收益為多少元?
(Ⅱ) 期中考試以后,學校決定將誠信用水的收益,以獎學金的形式獎勵給品學兼優的特困生,規定:特困生考入年級前200名,獲一等獎學金500元;考入年級201—500 名,獲二等獎學金300元;考入年級501名以后的特困生將不獲得獎學金。甲、乙兩名學生獲一等獎學金的概率均為![]() ,獲二等獎學金的概率均為
,獲二等獎學金的概率均為![]() ,不獲得獎學金的概率均為
,不獲得獎學金的概率均為![]() .
.
⑴在學生甲獲得獎學金條件下,求他獲得一等獎學金的概率;
⑵已知甲、乙兩名學生獲得哪個等第的獎學金是相互獨立的,求甲、乙兩名學生所獲得獎學金總金額X 的分布列及數學期望。
附: 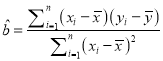 ,
, ![]() 。
。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線y2=2px的焦點為F,準線方程是x=﹣1.
(I)求此拋物線的方程;
(Ⅱ)設點M在此拋物線上,且|MF|=3,若O為坐標原點,求△OFM的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題正確的選項為( )
①平面外一條直線與平面內的一條直線平行,則該直線與此平面平行;
②一個平面內的一條直線與另一個平面平行,則這兩個平面平行;
③一條直線與一個平面內的兩條直線垂直,則該直線與此平面垂直;
④一個平面過另一個平面的垂線,則這兩個平面垂直.
A.①②B.②③C.①④D.③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校藝術節對![]() 四件參賽作品只評一件一等獎,在評獎揭曉前,甲,乙,丙,丁四位同學對這四件參賽作品預測如下:
四件參賽作品只評一件一等獎,在評獎揭曉前,甲,乙,丙,丁四位同學對這四件參賽作品預測如下:
甲說:“是![]() 或
或![]() 作品獲得一等獎”; 乙說:“
作品獲得一等獎”; 乙說:“ ![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“ ![]() 兩件作品未獲得一等獎”; 丁說:“是
兩件作品未獲得一等獎”; 丁說:“是![]() 作品獲得一等獎”.
作品獲得一等獎”.
評獎揭曉后,發現這四位同學中只有兩位說的話是對的,則獲得一等獎的作品是_________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 、
、![]() 為平面上兩個點集,滿足
為平面上兩個點集,滿足![]() ,
,![]() ,且任意三點不共線.在集合
,且任意三點不共線.在集合![]() 和
和![]() 間各連若干條線段,每條線段均一個端點在集合
間各連若干條線段,每條線段均一個端點在集合![]() 中,另一個端點在集合
中,另一個端點在集合![]() 中,且任意兩點間至多連一條線段,記所有線段構成的集合為
中,且任意兩點間至多連一條線段,記所有線段構成的集合為![]() .若集合
.若集合![]() 滿足對于集合
滿足對于集合![]() 或
或![]() 中任意一點均至少連出
中任意一點均至少連出![]() 條線段,則稱集合
條線段,則稱集合![]() 是“
是“![]() 一好的”.試確定
一好的”.試確定![]() 的最大值,使得去掉任意一條線段,集合
的最大值,使得去掉任意一條線段,集合![]() 均不是
均不是![]() 一好的.
一好的.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com