
【題目】已知![]() 為坐標原點,橢圓
為坐標原點,橢圓![]() :
: ![]() 的左焦點是
的左焦點是![]() ,離心率為
,離心率為![]() ,且
,且![]() 上任意一點
上任意一點![]() 到
到![]() 的最短距離為
的最短距離為![]() .
.
(1)求![]() 的方程;
的方程;
(2)過點![]() 的直線
的直線![]() (不過原點)與
(不過原點)與![]() 交于兩點
交于兩點![]() 、
、![]() ,
, ![]() 為線段
為線段![]() 的中點.
的中點.
(i)證明:直線![]() 與
與![]() 的斜率乘積為定值;
的斜率乘積為定值;
(ii)求![]() 面積的最大值及此時
面積的最大值及此時![]() 的斜率.
的斜率.
【答案】(1)![]() ;(2)(i)見解析;(ii)
;(2)(i)見解析;(ii)![]() 面積的最大值是
面積的最大值是![]() ,此時
,此時![]() 的斜率為
的斜率為![]() .
.
【解析】試題分析:(1)由題設可以得到關于![]() 的方程組為
的方程組為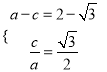 ,從而
,從而 ,故
,故![]() ,所以橢圓
,所以橢圓![]() 的方程為
的方程為![]() .(2)設直線
.(2)設直線![]() 為:
為: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,聯立直線的方程和橢圓的方程并消元后可以得到
,聯立直線的方程和橢圓的方程并消元后可以得到![]() ,利用韋達定理得到
,利用韋達定理得到![]() ,故
,故![]() ,從而
,從而![]() 為定值.利用弦長公式和點到直線的距離可得
為定值.利用弦長公式和點到直線的距離可得![]() ,令
,令![]() ,從而
,從而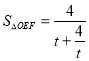 ,最后利用基本不等式可以得到面積的最大值為
,最后利用基本不等式可以得到面積的最大值為![]() 且此時
且此時![]() 也就是
也就是![]() .
.
解析:(1)由題意得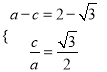 ,解得
,解得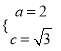 ,∴
,∴![]() ,
, ![]() ,∴橢圓
,∴橢圓![]() 的方程為
的方程為![]() .
.
(2)(i)設直線![]() 為:
為: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,由題意得
,由題意得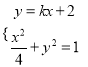 ,
,
∴![]() ,∴
,∴![]() ,即
,即![]() ,由韋達定理得:
,由韋達定理得: ![]() ,
, ![]() ,∴
,∴![]() ,
, ![]() ,∴
,∴![]() ,∴
,∴![]() ,∴直線
,∴直線![]() 與
與![]() 的斜率乘積為定值.
的斜率乘積為定值.

(ii)由(i)可知: ![]()
![]()
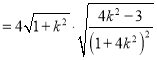
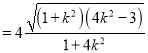 ,又點
,又點![]() 到直線
到直線![]() 的距離
的距離![]() ,
,
∴![]() 的面積
的面積![]()
![]()

![]() ,令
,令![]() ,則
,則![]() ,∴
,∴![]()
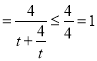 ,當且僅當
,當且僅當![]() 時等號成立,此時
時等號成立,此時![]() ,且滿足
,且滿足![]() ,∴
,∴![]() 面積的最大值是
面積的最大值是![]() ,此時
,此時![]() 的斜率為
的斜率為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數(x)=xlnx,g(x)=ax3-![]() .
.
(Ⅰ)求函數(x)的單調遞增區間和最小值;
(Ⅱ)若函數y= (x)與函數y =g(x)的圖象在交點處存在公共切線,求實數a的值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() 、
、![]() 為常數).若函數
為常數).若函數![]() 與
與![]() 的圖象在
的圖象在![]() 處相切,
處相切,
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)設函數![]()
![]() ,若
,若![]() 在
在![]() 上的最小值為
上的最小值為![]() ,求實數
,求實數![]() 的值;
的值;
(Ⅲ)設函數![]() ,若
,若![]() 在
在![]() 上恒成立,求實數
上恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() :
: ![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,上頂點為
,上頂點為![]() ,過點
,過點![]() 與
與![]() 垂直的直線交
垂直的直線交![]() 軸負半軸于點
軸負半軸于點![]() ,且
,且![]() .
.
(Ⅰ)求橢圓![]() 的離心率;
的離心率;
(Ⅱ)若過![]() 、
、![]() 、
、![]() 三點的圓恰好與直線
三點的圓恰好與直線![]() :
: ![]() 相切,求橢圓
相切,求橢圓![]() 的方程;
的方程;
(III)在(Ⅱ)的條件下,過右焦點![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點,在
兩點,在![]() 軸上是否存在點
軸上是否存在點![]() 使得以
使得以![]() 為鄰邊的平行四邊形是菱形,如果存在,求出
為鄰邊的平行四邊形是菱形,如果存在,求出![]() 的取值范圍,如果不存在,說明理由
的取值范圍,如果不存在,說明理由
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某P2P平臺需要了解該平臺投資者的大致年齡分布,發現其投資者年齡大多集中在區間[20,50]歲之間,對區間[20,50]歲的人群隨機抽取20人進行了一次理財習慣調查,得到如下統計表和各年齡段人數頻率分布直方圖:
組數 | 分組 | 人數(單位:人) |
第一組 | [20,25) | 2 |
第二組 | [25,30) | a |
第三組 | [30,35) | 5 |
第四組 | [35,40) | 4 |
第五組 | [40,45) | 3 |
第六組 | [45,50] | 2 |

(Ⅰ)求a的值并畫出頻率分布直方圖;
(Ⅱ)在統計表的第五與第六組的5人中,隨機選取2人,求這2人的年齡都小于45歲的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設 ![]() 為橢圓
為橢圓 ![]() 上任一點,
上任一點,![]() ,
,![]() 為橢圓的焦點,
為橢圓的焦點,![]() ,離心率為
,離心率為 ![]() .
.
(1)求橢圓的標準方程;
(2)直線 ![]() 經過點
經過點 ![]() ,且與橢圓交于
,且與橢圓交于 ![]() ,
,![]() 兩點,若直線
兩點,若直線 ![]() ,
,![]() ,
,![]() 的斜率依次成等比數列,求直線
的斜率依次成等比數列,求直線 ![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】大西洋鮭魚每年都要逆流而上,游回產地產卵,經研究發現鮭魚的游速可以表示為函數y=![]() log3(
log3(![]() ),單位是m/s,θ是表示魚的耗氧量的單位數.
),單位是m/s,θ是表示魚的耗氧量的單位數.
(1)當一條鮭魚的耗氧量是900個單位時,它的游速是多少?
(2)計算一條魚靜止時耗氧量的單位數。
(3)某條鮭魚想把游速提高1 m/s,那么它的耗氧量的單位數是原來的多少倍?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com