
設函數 ,其中mÎ
R,集合M={m|m>1}.
,其中mÎ
R,集合M={m|m>1}.
(1)求證:當mÎ M時,f(x)對所有實數x都有意義;反之,如果f(x)對所有實數x都有意義,那么mÎ M.
(2)當mÎ M時,求函數f(x)的最小值.
(3)求證:對每一個mÎ M,函數f(x)的最小值都不小于1.
|
本題中所給函數是二次函數和對數函數的復合函數,因此在解答過程中應注意二次函數與對數函數性質的應用. (1) 證明:當mÎ M時,有m>1,從而對所有實數x,都有: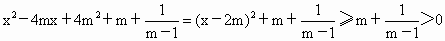 . .
∴當 mÎ M時,函數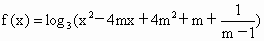 對所有的實數x都有意義. 對所有的實數x都有意義.
反之,如果 f(x)對所有實數x都有意義,則需對所有實數x,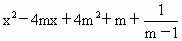 恒大于0, 恒大于0,
∵ 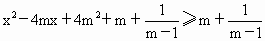 , ,
∴應使 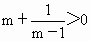 ,即 ,即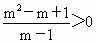 . .
由于 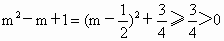 ,又必須m-1>0,即m>1. ,又必須m-1>0,即m>1.
從而 mÎ M.(2) ∵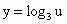 在(0,+∞)上是增函數,由(1)可知,當mÎ
M時, 在(0,+∞)上是增函數,由(1)可知,當mÎ
M時, , ,
∴ 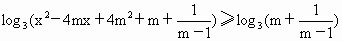 . .
又當 x=2m時,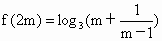 . .
∴當 mÎ M時,f(x)的最小值為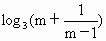 . .
(3) 當mÎ M時,有m>1,∴m-1>0.此時  ,且在m=2時,取“=”號. ,且在m=2時,取“=”號.
∴  .∴ .∴ , ,
即對于每一個 mÎ M,函數f(x)的最小值都不小于1.在解答第 (1)問的過程中,兩次使用配方法,即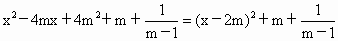 和 和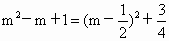 .在解答第(3)問時,也用了配方法,即 .在解答第(3)問時,也用了配方法,即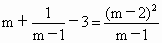 .用配方法是解決二次函數問題的重要手段. .用配方法是解決二次函數問題的重要手段. |


 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:高中數學 來源: 題型:044
設函數
 ,其中mÎ
R,集合M={m|m>1}.
,其中mÎ
R,集合M={m|m>1}.
(1)
求證:當mÎ M時,f(x)對所有實數x都有意義;反之,如果f(x)對所有實數x都有意義,那么mÎ M.(2)
當mÎ M時,求函數f(x)的最小值.(3)
求證:對每一個mÎ M,函數f(x)的最小值都不小于1.查看答案和解析>>
科目:高中數學 來源:2011-2012學年江西省、遂川中學高三聯考文科數學 題型:解答題
(本小題滿分12分)已知二次函數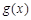 的圖像經過坐標原點,且滿足
的圖像經過坐標原點,且滿足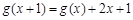 ,設函數
,設函數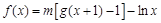 ,其中m為常數且
,其中m為常數且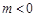 。
。
(1)求函數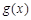 的解析式;
的解析式;
(2)判斷函數 的單調性并說明理由。
的單調性并說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
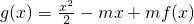 ,其中m為常數.
,其中m為常數.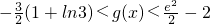 成立.
成立.查看答案和解析>>
科目:高中數學 來源:2012-2013學年高一年級(上)期中數學試卷(解析版) 題型:解答題
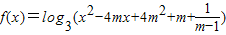 ,其中m是實數,設M={m|m>1}
,其中m是實數,設M={m|m>1}查看答案和解析>>
科目:高中數學 來源:2012年福建省寧德市高三畢業班質量檢查數學試卷(文科)(解析版) 題型:解答題
 ,其中m為常數.
,其中m為常數. 成立.
成立.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com