
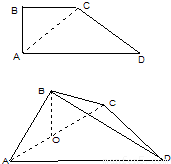
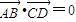 ,可得AB⊥CD,再利用AB⊥BC,可得AB⊥平面BCD;
,可得AB⊥CD,再利用AB⊥BC,可得AB⊥平面BCD;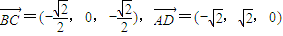 ,利用向量夾角公式,可求異面直線BC與AD所成的角;
,利用向量夾角公式,可求異面直線BC與AD所成的角; ,平面ABD的法向量
,平面ABD的法向量 ,利用向量夾角公式,可求二面角B-AD-C的平面角;
,利用向量夾角公式,可求二面角B-AD-C的平面角;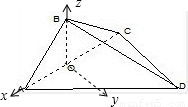 解法1:(Ⅰ)在梯形ABCD中,∵
解法1:(Ⅰ)在梯形ABCD中,∵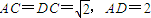 ,∴AC2+DC2=AD2,∴AC⊥DC.
,∴AC2+DC2=AD2,∴AC⊥DC.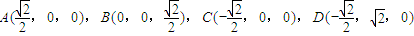 ,
,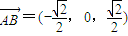 ,
,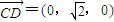 ,∴
,∴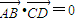 ,∴AB⊥CD,
,∴AB⊥CD,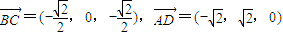 ,∴
,∴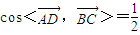 ,
,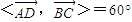 ,即異面直線BC與AD所成的角為60°.…(9分)
,即異面直線BC與AD所成的角為60°.…(9分)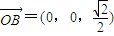 .
.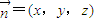 ,則
,則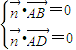 ,即
,即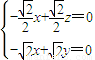 ,解得
,解得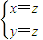 ,
,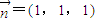 .
.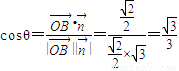 .…(12分)
.…(12分)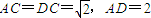 ,∴AC2+DC2=AD2,∴AC⊥DC.
,∴AC2+DC2=AD2,∴AC⊥DC.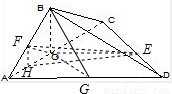
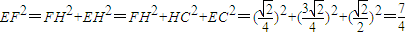 ,
,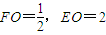 ,∴
,∴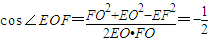 ,
,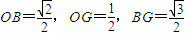 ,∴
,∴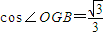 .…(12分)
.…(12分)

 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
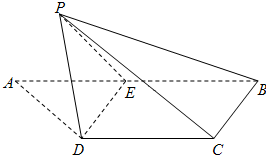 如圖,梯形ABCD中,CD∥AB,AD=DC=CB=
如圖,梯形ABCD中,CD∥AB,AD=DC=CB=| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,梯形ABCD中,AD∥BC,PA⊥平面ABCD,E是PD的中點,AB=BC=1,PA=AD=2.
如圖,梯形ABCD中,AD∥BC,PA⊥平面ABCD,E是PD的中點,AB=BC=1,PA=AD=2.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,梯形ABCD中,CD∥AB,AD=DC=CB=
如圖,梯形ABCD中,CD∥AB,AD=DC=CB=| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
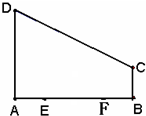 如圖直角梯形ABCD中,∠DAB=90°,AD∥BC,E,F是AB邊的四等分點,AB=4,BC=BF=AE=1,AD=3,P為在梯形區域內一動點,滿足PE+PF=AB,記動點P的軌跡為Γ.
如圖直角梯形ABCD中,∠DAB=90°,AD∥BC,E,F是AB邊的四等分點,AB=4,BC=BF=AE=1,AD=3,P為在梯形區域內一動點,滿足PE+PF=AB,記動點P的軌跡為Γ.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com