
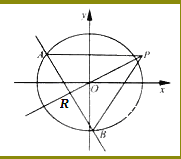
【題目】如圖,橢圓C: ![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,其左焦點到點
,其左焦點到點![]() 的距離為
的距離為![]() .不過原點O的直線
.不過原點O的直線![]() 與C相交于A,B兩點,且線段AB被直線OP平分.
與C相交于A,B兩點,且線段AB被直線OP平分.
(1)求橢圓C的方程;
(2)求![]() ABP的面積取最大時直線l的方程.
ABP的面積取最大時直線l的方程.
【答案】(1) ![]() ;(2) 直線l的方程為
;(2) 直線l的方程為![]()
![]() .
.
【解析】試題分析:
(1)由題意可得![]() .則所求橢圓C的方程為:
.則所求橢圓C的方程為: ![]() .
.
(2)首先設出點的坐標,設而不求可得直線AB的斜率為![]() ,然后聯立直線與橢圓的方程,結合面積函數,利用導函數研究三角形面積的最大值可得
,然后聯立直線與橢圓的方程,結合面積函數,利用導函數研究三角形面積的最大值可得![]() ABP的面積取最大時直線l的方程是
ABP的面積取最大時直線l的方程是![]()
![]() .
.
試題解析:
(1)由題意可得: ![]() ①;
①;
左焦點![]() 到點
到點![]() 的距離為:
的距離為: ![]()
![]() ②.
②.
由①②可解得: ![]() .
.
∴所求橢圓C的方程為: ![]() .
.
(2)易得直線OP的方程: ![]() ,設A(xA,yA),B(xB,yB),R(x0,y0).
,設A(xA,yA),B(xB,yB),R(x0,y0).
其中y0=![]() x0.∵A,B在橢圓上,
x0.∵A,B在橢圓上,
∴ .
.
設直線AB的方程為![]() (m≠0),代入橢圓:
(m≠0),代入橢圓: 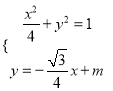 ,
,
整理得: ![]() .
.
顯然![]() .
.
∴﹣![]() 且m≠0.由上又有:
且m≠0.由上又有: ![]() ,
, ![]() .
.
∴AB=![]() |
|![]() |=
|=![]()
![]() =
=![]()
![]() .
.
∵點![]() 到直線l的距離表示為:
到直線l的距離表示為: 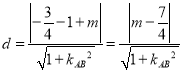 .
.
∴S![]() ABP=
ABP=![]()
![]() =
=![]()
![]() ,
,
令![]() ,
,
則![]() ,
,
﹣![]() 且m≠0,
且m≠0, ![]() ,令
,令![]() 則
則![]() ,
,
解得![]() ,(
,( ![]() ),
),
當![]() 時,
時, ![]()
![]() 遞增,
遞增,
當![]() 時,
時, ![]()
![]() 遞減,
遞減,
所以,當且僅當![]() 時,
時, ![]() ABP的面積取最大,
ABP的面積取最大,
此時,直線l的方程為![]()
![]() .
.


科目:高中數學 來源: 題型:
【題目】據統計,2016年“雙十”天貓總成交金額突破1207億元.某購物網站為優化營銷策略,對11月11日當天在該網站進行網購消費且消費金額不超過1000元的1000名網購者(其中有女性800名,男性200名)進行抽樣分析.采用根據性別分層抽樣的方法從這1000名網購者中抽取100名進行分析,得到下表:(消費金額單位:元)
女性消費情況:
消費金額 |
|
|
|
|
|
人數 | 5 | 10 | 15 | 47 |
|
男性消費情況:
消費金額 |
|
|
|
|
|
人數 | 2 | 3 | 10 |
| 2 |
(1)計算![]() ,
,![]() 的值;在抽出的100名且消費金額在
的值;在抽出的100名且消費金額在![]() (單位:元)的網購者中隨機選出兩名發放網購紅包,求選出的兩名網購者恰好是一男一女的概率;
(單位:元)的網購者中隨機選出兩名發放網購紅包,求選出的兩名網購者恰好是一男一女的概率;
(2)若消費金額不低于600元的網購者為“網購達人”,低于600元的網購者為“非網購達人”,根據以上統計數據填寫![]() 列聯表,并回答能否在犯錯誤的概率不超過0.010的前提下認為“是否為‘網購達人’與性別有關?”
列聯表,并回答能否在犯錯誤的概率不超過0.010的前提下認為“是否為‘網購達人’與性別有關?”
女性 | 男性 | 總計 | |
網購達人 | |||
非網購達人 | |||
總計 |
附:
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列哪組中的函數f(x)與g(x)相等( )
A.f(x)=x2 , ![]()
B.f(x)=x+1,g(x)= ![]() +1
+1
C.f(x)=x,g(x)= ![]()
D.f(x)= ![]() ,g(x)=
,g(x)= ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex﹣1﹣x.
(1)若存在x∈[﹣1,ln ![]() ],滿足a﹣ex+1+x<0成立,求實數a的取值范圍.
],滿足a﹣ex+1+x<0成立,求實數a的取值范圍.
(2)當x≥0時,f(x)≥(t﹣1)x恒成立,求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩條直線l1:y=a和l2:y= ![]() (其中a>0),若直線l1與函數y=|log4x|的圖象從左到右相交于點A,B,直線l2與函數y=|log4x|的圖象從左到右相交于點C,D.記線段AC和BD在x軸上的投影長度分別為 m,n.令f(a)=log4
(其中a>0),若直線l1與函數y=|log4x|的圖象從左到右相交于點A,B,直線l2與函數y=|log4x|的圖象從左到右相交于點C,D.記線段AC和BD在x軸上的投影長度分別為 m,n.令f(a)=log4 ![]() .
.
(1)求f(a)的表達式;
(2)當a變化時,求出f(a)的最小值,并指出取得最小值時對應的a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位組織職工去某地參觀學習,需包車前往,甲車隊說:“如果領隊買一張全票,其余人可享受7折優惠。”乙車隊說:“你們屬于團體票,按原價的7.5折優惠。”這兩個車隊的原價、車型都是一樣的,試根據單位去的人數比較兩車隊的收費哪家更優惠。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,一根水平放置的長方體枕木的安全負荷與它的厚度d的平方和寬度a的乘積成正比,與它的長度l的平方成反比. 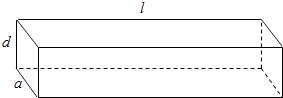
(1)在a>d>0的條件下,將此枕木翻轉90°(即寬度變為了厚度),枕木的安全負荷會發生變化嗎?變大還是變小?
(2)現有一根橫截面為半圓(半圓的半徑為R= ![]() )的柱形木材,用它截取成橫截面為長方形的枕木,其長度即為枕木規定的長度l,問橫截面如何截取,可使安全負荷最大?
)的柱形木材,用它截取成橫截面為長方形的枕木,其長度即為枕木規定的長度l,問橫截面如何截取,可使安全負荷最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】共享單車是指企業在校園、地鐵站點、公交站點、居民區、商業區、公共服務區等提供自行車單車共享服務,是共享經濟的一種新形態,一個共享單車企業在某個城市就“一天中一輛單車的平均成本(單位:元)與租用單車的數量(單位:車輛)之間的關系”進行調查研究,在調查過程中進行了統計,得出相關數據見下表:
租用單車數量 | 2 | 3 | 4 | 5 | 8 |
每天一輛車平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
根據以上數據,研究人員分別借助甲、乙兩種不同的回歸模型,得到兩個回歸方程,方程甲: ![]() ,方程乙:
,方程乙: ![]() .
.
(1)為了評價兩種模型的擬合效果,完成以下任務:
①完成下表(計算結果精確到0.1)(備注: ![]() ,
, ![]() 稱為相應于點
稱為相應于點![]() 的殘差(也叫隨機誤差));
的殘差(也叫隨機誤差));
租用單車數量 | 2 | 3 | 4 | 5 | 8 | |
每天一輛車平均成本 | 3.2 | 2 | 1.9 | 1.7 | ||
模型甲 | 估計值 | 2.4 | 2.1 | 1.6 | ||
殘差 | 0 |
| 0.1 | |||
模型乙 | 估計值 | 2.3 | 2 | 1.9 | ||
殘差 | 0.1 | 0 | 0 | |||
②分別計算模型甲與模型乙的殘差平方和![]() 及
及![]() ,并通過比較
,并通過比較![]() ,
, ![]() 的大小,判斷哪個模型擬合效果更好.
的大小,判斷哪個模型擬合效果更好.
(2)這個公司在該城市投放共享單車后,受到廣大市民的熱烈歡迎,共享單車常常供不應求,于是該公司研究是否增加投放,根據市場調查,這個城市投放8千輛時,該公司平均一輛單一天能收入10元,6元收入的概率分別為0.6,0.4;投放1萬輛時,該公司平均一輛單車一天能收入10元,6元收入的概率分別為0.4,0.6,問該公司應該投放8千輛還是1萬輛能獲得更多利潤?(按(1)中擬合效果較好的模型計算一天中一輛單車的平均成本,利潤=收入—成本).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】命題p:關于x的不等式x2+(a﹣1)x+a2<0的解集是空集,命題q:已知二次函數f(x)=x2﹣mx+2滿足 ![]() ,且當x∈[0,a]時,最大值是2,若命題“p且q”為假,“p或q”為真,求實數a的取值范圍.
,且當x∈[0,a]時,最大值是2,若命題“p且q”為假,“p或q”為真,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com