設等差數(shù)列{
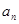
}的前

項和為

,已知

=

,

.
(Ⅰ) 求數(shù)列{
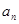
}的通項公式;
(Ⅱ)求數(shù)列{
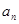
}的前n項和

;
(Ⅲ)當n為何值時,

最大,并求

的最大值.
(Ⅰ)
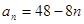
(Ⅱ)

=
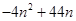
(Ⅲ)當
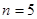
或
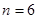
時,

最大,且

的最大值為120.
試題分析:(Ⅰ)依題意有
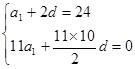
,解之得
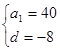
,∴
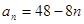
.
(Ⅱ)由(Ⅰ)知,
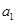
=40,
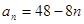
,
∴

=
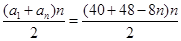
=
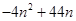
.
(Ⅲ)由(Ⅱ)有,

=
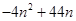
=-4
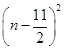
+121,
故當
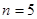
或
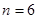
時,

最大,且

的最大值為120.
點評:等差數(shù)列是一類比較重要的數(shù)列,它的基本量之間的關系經(jīng)常考查,要牢固掌握它們之間的關系,靈活求解.
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
在數(shù)列
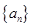
中,對于任意
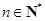
,等式:

恒成立,其中常數(shù)

.
(1)求
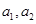
的值;
(2)求證:數(shù)列
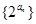
為等比數(shù)列;
(3)如果關于

的不等式
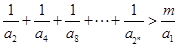
的解集為
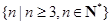
,試求實數(shù)
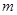
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
等差數(shù)列

項的和

等于
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知數(shù)列

滿足

,

,則該數(shù)列的通項公式

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
各項均為正數(shù)的等差數(shù)列

首項為1,且

成等比數(shù)列,

(1)求

、

通項公式;
(2)求數(shù)列

前n項和

;
(3)若對任意正整數(shù)n都有

成立,求

范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知數(shù)列
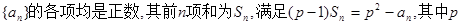
為正常數(shù),且
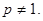
(1)求數(shù)列
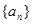
的通項公式;
(2)設
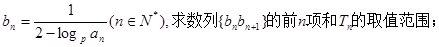
(3)是否存在正整數(shù)M,使得
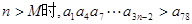
恒成立?若存在,求出相應的M的最小值;若不存在,請說明理由。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知等差數(shù)列
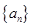
的前
n項和為
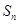 ,
,且滿足
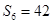
,
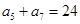
.
(1)求數(shù)列
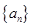
的通項
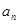
及前
n項和
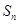
;
(2)令
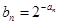
(
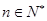
),求數(shù)列
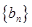
的前
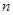
項和
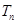
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知數(shù)列
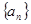
的前項和為
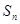
,滿足
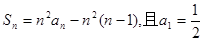
,
(1)令
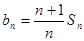
,證明:
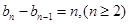
;
(2)求數(shù)列
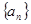
的通項公式。
查看答案和解析>>

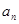 }的前
}的前 項和為
項和為 ,已知
,已知 =
= ,
, .
.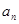 }的通項公式;
}的通項公式;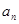 }的前n項和
}的前n項和 ;
; 最大,并求
最大,并求 的最大值.
的最大值.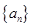 中,對于任意
中,對于任意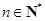 ,等式:
,等式: 恒成立,其中常數(shù)
恒成立,其中常數(shù) .
.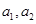 的值;
的值; 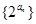 為等比數(shù)列;
為等比數(shù)列; 的不等式
的不等式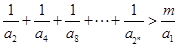 的解集為
的解集為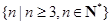 ,試求實數(shù)
,試求實數(shù)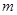 的取值范圍.
的取值范圍. 首項為1,且
首項為1,且 成等比數(shù)列,
成等比數(shù)列,
 、
、 通項公式;
通項公式; 前n項和
前n項和 ;
; 成立,求
成立,求 范圍.
范圍.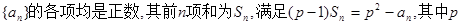 為正常數(shù),且
為正常數(shù),且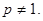
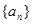 的通項公式;
的通項公式;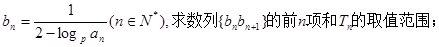
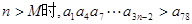 恒成立?若存在,求出相應的M的最小值;若不存在,請說明理由。
恒成立?若存在,求出相應的M的最小值;若不存在,請說明理由。