Question

已知實數x，y滿足2x+y≥1，則u=x²+y²+4x-2y的最小值為

-

9

5

．

Answer 1

分析：根據題意，設點P（x，y），它在區域2x+y≥1內運動，u表示點P（x，y）與定點A（-2，1）的距離的平方與5的差，問題轉化為求定點A（-2，1）到由2x+y≥1所確定的平面區域的最近距離，故A到直線l的距離為A到區域G上點的距離的最小值，由此結合點到直線l的距離公式，即可得到u的最小值．

解答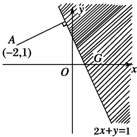：解析：由u=x²+y²+4x-2y=（x+2）²+（y-1）²-5
知，u表示點P（x，y）與定點A（-2，1）的距離的平方與5的差．
又由約束條件2x+y≥1知：
點P（x，y）在直線l：2x+y=1上及其右上方．
問題轉化為求定點A（-2，1）到由2x+y≥1所確定的平面區域的最近距離．
故A到直線l的距離為A到區域G上點的距離的最小值．
d=

|2×?-2?+1-1|

22+12

=

4

5

，
∴d²=

16

5

，
∴u_min=d²-5=-

9

5

．
故答案：-

9

5

點評：本題給出實數x、y滿足一次關系式，求它們平方和的最小值，著重考查了坐標系內簡單線性規劃的應用和點到直線的距離公式等知識，屬于基礎題．