
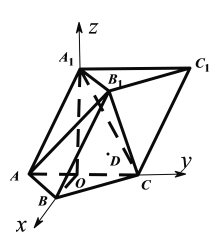
【題目】如圖,三棱柱![]() 中,側面
中,側面![]() 底面
底面![]() ,
,![]() 是邊長為2的正三角形,已知
是邊長為2的正三角形,已知![]() 點滿足
點滿足![]() .
.
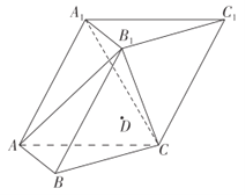
(1)求二面角![]() 的大小;
的大小;
(2)求異面直線![]() 與
與![]() 的距離;
的距離;
(3)直線![]() 上是否存在點
上是否存在點![]() ,使
,使![]() 平面?若存在,請確定點
平面?若存在,請確定點![]() 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.
【答案】(1)![]() (2)
(2)![]() (3)存在點
(3)存在點![]() ,其坐標為
,其坐標為![]() ,即恰好為
,即恰好為![]() 點
點
【解析】
(1)建立空間直角坐標系,利用平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,計算出二面角
的法向量,計算出二面角![]() 的余弦值,由此求得其大小.
的余弦值,由此求得其大小.
(2)求得異面直線![]() 與
與![]() 的公垂線的方向向量,并由此計算出異面直線
的公垂線的方向向量,并由此計算出異面直線![]() 與
與![]() 的距離.
的距離.
(3)根據![]() 求得
求得![]() 點的坐標,設出
點的坐標,設出![]() 點的坐標,根據
點的坐標,根據![]() 、
、![]() 與平面
與平面![]() 的法向量垂直列方程組,解方程組求得
的法向量垂直列方程組,解方程組求得![]() 點的坐標,由此判斷出存在
點的坐標,由此判斷出存在![]() 點符合題意.
點符合題意.
(1)![]() 側面
側面![]() 底面
底面![]() ,又
,又![]() 均為正三角形,取
均為正三角形,取![]() 得中點
得中點![]() ,連接
,連接![]() ,
,![]() ,
,
則![]() 底面
底面![]() ,
,![]()
故以![]() 為坐標原點,分別以
為坐標原點,分別以![]() 為
為![]() 軸、
軸、![]() 軸、
軸、![]() 軸建立
軸建立![]() 如圖所示空間直角坐標系,
如圖所示空間直角坐標系,
則![]()
![]()
![]()
![]()
設平面![]() 的法向量為
的法向量為![]()
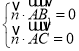
取![]() ,可得
,可得![]()
又平面![]() 的一個法向量為
的一個法向量為![]()
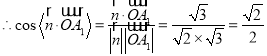
由圖知二面角![]() 為銳角,故二面角
為銳角,故二面角![]() 的大小為
的大小為![]() .
.
(2)異面直線![]() 與
與![]() 的公垂線的方向向量
的公垂線的方向向量![]() ,則
,則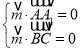
易得![]() ,異面直線
,異面直線![]() 與
與![]() 的距離
的距離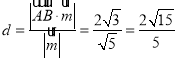
(3)![]() ,而
,而![]()
![]()
又![]() ,
,![]() 點
點![]() 的坐標為
的坐標為![]()
假設存在點![]() 符合題意,則點
符合題意,則點![]() 的坐標可設為
的坐標可設為![]()
![]()
![]() 平面
平面![]()
![]() 為平面
為平面![]() 的一個法向量,
的一個法向量,
![]() 由
由![]() ,得
,得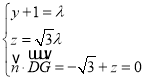
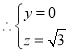 .
.
又![]() 平面
平面![]() ,
,
故存在點![]() ,使
,使![]() 平面
平面![]() ,其坐標為
,其坐標為![]() ,即恰好為
,即恰好為![]() 點.
點.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() :
:![]() (
(![]() 為參數,
為參數,![]() ),曲線
),曲線![]() :
:![]() (
(![]() 為參數),
為參數),![]() 與
與![]() 相切于點
相切于點![]() ,以坐標原點為極點,
,以坐標原點為極點,![]() 軸的非負半軸為極軸建立極坐標系.
軸的非負半軸為極軸建立極坐標系.
(1)求![]() 的極坐標方程及點
的極坐標方程及點![]() 的極坐標;
的極坐標;
(2)已知直線![]() :
:![]() 與圓
與圓![]() :
:![]() 交于
交于![]() ,
,![]() 兩點,記
兩點,記![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】大慶實驗中學在高二年級舉辦線上數學知識競賽,在已報名的400名學生中,根據文理學生人數比例,使用分層抽樣的方法從中隨機抽取了100名學生,記錄他們的分數,將數據分成7組:[20,30),[30,40),…,[80,90],并整理得到如下頻率分布直方圖:
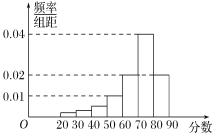
(1)估算一下本次參加考試的同學成績的中位數和眾數;
(2)已知樣本中分數小于40的學生有5人,試估計總體中分數在區間[40,50)內的人數;
(3)已知樣本中有一半理科生的分數不小于70,且樣本中分數不小于70的文理科生人數相等.試估計總體中理科生和文科生人數的比例.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據國家統計局數據,1978年至2018年我國GDP總量從0.37萬億元躍升至90萬億元,實際增長了242倍多,綜合國力大幅提升.
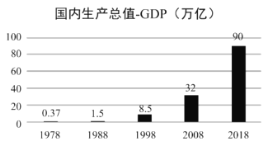
將年份1978,1988,1998,2008,2018分別用1,2,3,4,5代替,并表示為![]() ;
;![]() 表示全國GDP總量,表中
表示全國GDP總量,表中![]() ,
,![]() .
.
|
|
|
|
|
|
3 | 26.474 | 1.903 | 10 | 209.76 | 14.05 |
(1)根據數據及統計圖表,判斷![]() 與
與![]() (其中
(其中![]() 為自然對數的底數)哪一個更適宜作為全國GDP總量
為自然對數的底數)哪一個更適宜作為全國GDP總量![]() 關于
關于![]() 的回歸方程類型?(給出判斷即可,不必說明理由),并求出
的回歸方程類型?(給出判斷即可,不必說明理由),并求出![]() 關于
關于![]() 的回歸方程.
的回歸方程.
(2)使用參考數據,估計2020年的全國GDP總量.
線性回歸方程![]() 中斜率和截距的最小二乘法估計公式分別為:
中斜率和截距的最小二乘法估計公式分別為:
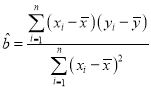 ,
,![]() .
.
參考數據:
| 4 | 5 | 6 | 7 | 8 |
| 55 | 148 | 403 | 1097 | 2981 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC-A1B1C1中,D,E分別為AB,BC的中點,點F在側棱B1B上,且![]() ,
, ![]() .
.

求證:(1)直線DE![]() 平面A1C1F;
平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為圓
為圓![]() 上的動點,點
上的動點,點![]() 在圓的半徑
在圓的半徑![]() 上運動,點
上運動,點![]() 在
在![]() 上,且滿足
上,且滿足![]() ,其中
,其中![]() .
.
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)設不過原點![]() 的直線與
的直線與![]() 點的軌跡交于
點的軌跡交于![]() 兩點,且點
兩點,且點![]() 關于恒過定點
關于恒過定點![]() 的直線
的直線![]() 對稱.求
對稱.求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 是等比數列,有下列四個命題:①
是等比數列,有下列四個命題:①![]() 是等比數列;②
是等比數列;②![]() 是等比數列;③
是等比數列;③![]() 是等比數列;④
是等比數列;④![]() 是等比數列,其中正確命題的序號是( )
是等比數列,其中正確命題的序號是( )
A.②④B.③④C.②③④D.①②③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com