
【題目】為了弘揚中華民族傳統文化,某中學高二年級舉行了“愛我中華,傳誦經典”的考試,并從中隨機抽取了![]() 名學生的成績(滿分
名學生的成績(滿分![]() 分)作為樣本,其中成績不低于
分)作為樣本,其中成績不低于![]() 分的學生被評為優秀生,得到成績分布的頻率分布直方圖如圖所示.
分的學生被評為優秀生,得到成績分布的頻率分布直方圖如圖所示.
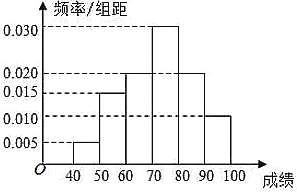
(1)若該年級共有![]() 名學生,試利用樣本估計該年級這次考試中優秀生人數;
名學生,試利用樣本估計該年級這次考試中優秀生人數;
(2)試估計這次參加考試的學生的平均成績(同一組數據用該組區間中點值作代表);
(3)若在樣本中,利用分層抽樣從成績不低于![]() 分的學生中隨機抽取
分的學生中隨機抽取![]() 人,再從中抽取
人,再從中抽取![]() 人贈送一套國學經典典籍,試求恰好抽中
人贈送一套國學經典典籍,試求恰好抽中![]() 名優秀生的概率.
名優秀生的概率.
【答案】(1)![]() 人;(2)
人;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由直方圖知,樣本中數據落在![]() 的頻率為
的頻率為![]() ,由此能估計全校這次考試中優秀生人數;
,由此能估計全校這次考試中優秀生人數;
(2)將每個矩形底邊的中點值乘以矩形的面積,再將所得結果相加即可得出樣本數據的平均數;
(3)由分層抽樣可知成績在![]() 、
、![]() 、
、![]() 間分別抽取了
間分別抽取了![]() 、
、![]() 、
、![]() 人,記成績在
人,記成績在![]() 的
的![]() 人為
人為![]() 、
、![]() 、
、![]() ,在
,在![]() 的
的![]() 人為
人為![]() 、
、![]() ,在
,在![]() 的
的![]() 人記為
人記為![]() ,列出所有的基本事件,利用古典概型的概率公式可求出所求事件的概率.
,列出所有的基本事件,利用古典概型的概率公式可求出所求事件的概率.
(1)由直方圖知,樣本中數據落在![]() 的頻率為:
的頻率為:![]() ,
,
則估計全校這次考試中優秀生人數為:![]() 人;
人;
(2)該樣本數據的平均數為:
![]() ,
,
![]() 估計所有參加考試的學生的平均成績為
估計所有參加考試的學生的平均成績為![]() ;
;
(3)由分層抽樣可知成績在![]() 、
、![]() 、
、![]() 間分別抽取了
間分別抽取了![]() 、
、![]() 、
、![]() 人,
人,
記成績在![]() 的
的![]() 人為
人為![]() 、
、![]() 、
、![]() ,在
,在![]() 的
的![]() 人為
人為![]() 、
、![]() ,在
,在![]() 的
的![]() 人記為
人記為![]() ,
,
則![]() 人中抽取
人中抽取![]() 人的所有情況有
人的所有情況有![]() 種,分別為:
種,分別為:
![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,
記抽取![]() 人為優秀生為事件
人為優秀生為事件![]() ,則事件
,則事件![]() 包含的基本事件有:
包含的基本事件有:![]() 、
、![]() 、
、![]() ,共
,共![]() 種,
種,
因此,恰好抽中![]() 名優秀生的概率
名優秀生的概率![]() .
.


 期末集結號系列答案
期末集結號系列答案科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為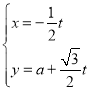 (
(![]() 為參數,
為參數,![]() ).以坐標原點為極點,
).以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,射線
,射線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,直線
兩點,直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點.
兩點.
(Ⅰ)求直線![]() 的普通方程和曲線C的直角坐標方程;
的普通方程和曲線C的直角坐標方程;
(Ⅱ)當![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年春節期間.當紅彩視明星翟天臨“不知“知網””學術不端事件在全國鬧得沸沸揚揚,引發了網友對亞洲最大電影學府北京電影學院、乃至整個中國學術界高等教育亂象的反思.為進一步端正學風,打擊學術造假行為,教育部日前公布的《教育部2019年部門預算》中透露,2019年教育部擬抽檢博士學位論文約6000篇,預算為800萬元.國務院學位委員會、教育部2014年印發的《博士碩士學位論文抽檢辦法》通知中規定:每篇抽檢的學位論文送3位同行專家進行評議,3位專家中有2位以上(含2位)專家評議意見為“不合格”的學位論文.將認定為“存在問題學位論文”。有且只有1位專家評議意見為“不合格”的學位論文,將再送2位同行專家進行復評.2位復評專家中有1位以上(含1位)專家評議意見為“不合格”的學位論文,將認定為“存在問題學位論文”。設毎篇學位論文被毎位專家評議為“不合格”的槪率均為![]() ,且各篇學位論文是否被評議為“不合格”相互獨立.
,且各篇學位論文是否被評議為“不合格”相互獨立.
(1)記一篇抽檢的學位論文被認定為“存在問題學位論文”的概率為![]() ,求
,求![]() ;
;
(2)若擬定每篇抽檢論文不需要復評的評審費用為900元,需要復評的評審費用為1500元;除評審費外,其它費用總計為100萬元。現以此方案實施,且抽檢論文為6000篇,問是否會超過預算?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() (a>b>0)的一個頂點為A(2,0),離心率為
(a>b>0)的一個頂點為A(2,0),離心率為![]() .直線y=k(x-1)與橢圓C交于不同的兩點M,N.
.直線y=k(x-1)與橢圓C交于不同的兩點M,N.
(1)求橢圓C的方程;
(2)當△AMN的面積為![]() 時,求k的值.
時,求k的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com