
【題目】已知函數![]() ,
,![]() .
.
(Ⅰ)討論![]() 的單調性;
的單調性;
(Ⅱ)![]() 使得
使得![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)答案不唯一,具體見解析(Ⅱ)![]() 或
或![]()
【解析】
(Ⅰ)求出函數的導數,通過討論![]() 的范圍,求出函數的單調區間即可。
的范圍,求出函數的單調區間即可。
(Ⅱ)由于![]() 時,
時,![]() ,若要
,若要![]() 使得
使得![]() 成立,只需
成立,只需![]() 時,
時,![]() 成立,利用導數討論
成立,利用導數討論![]() 的最大值和
的最大值和![]() 的最小值,即可求出實數
的最小值,即可求出實數![]() 的取值范圍。
的取值范圍。
(Ⅰ)由題可得![]() 的定義域為
的定義域為![]() ,
,![]()
![]() ,
,
當![]() 時,
時,![]() ,解得
,解得![]() ,或
,或![]() ,
,![]() ,解得
,解得![]() ,
,
∴![]() 在
在![]() ,
,![]() 上是增函數,在
上是增函數,在![]() 上是減函數;
上是減函數;
當![]() 時,
時,![]() ,解得
,解得![]() ,或
,或![]() ,
,![]() ,解得
,解得![]() ,
,
∴![]() 在
在![]() ,
,![]() 上是增函數,在
上是增函數,在![]() 上是減函數;
上是減函數;
當![]() 時,
時,![]() 恒成立,且只在
恒成立,且只在![]() 時
時![]() ,∴
,∴![]() 在
在![]() 上是增函數.
上是增函數.
(Ⅱ)![]() 時,
時,![]() ,
,
若要![]() 使得
使得![]() 成立,
成立,
只需![]() 時,
時,![]() 成立,
成立,
由(Ⅰ)知當![]() 時,
時,![]() 在
在![]() 上是增函數,
上是增函數,![]() ,
,
當![]() 時,
時,![]() 在
在![]() 上是減函數,在
上是減函數,在![]() 上是增函數,
上是增函數,
![]() ,
,
當![]() 時,
時,![]() 在
在![]() 上是減函數,
上是減函數,![]() ,
,
![]() ,對稱軸
,對稱軸![]() ,
,
當![]() 時,
時,![]() 在
在![]() 上是增函數,
上是增函數,![]() ,
,
![]() ,解得
,解得![]() ,∴
,∴![]() ,
,
當![]() 時,
時,![]() 在
在![]() 上是增函數,在
上是增函數,在![]() 上是減函數,
上是減函數,
![]() ,
,![]() ,
,
整理得![]() ,∵
,∵![]() ,∴只需
,∴只需![]() ,
,
令![]() ,
,![]() ,當
,當![]() 時,
時,![]() ,
,![]() 在
在![]() 上是增函數,又
上是增函數,又![]() ,∴
,∴![]() 時,
時,![]() ,∴
,∴![]() .
.
當![]() 時,
時,![]() 在
在![]() 上是減函數,
上是減函數,![]() ,
,
![]() ,解得
,解得![]() ,
,
綜上所述,![]() 或
或![]() .
.


 新黃岡兵法密卷系列答案
新黃岡兵法密卷系列答案科目:高中數學 來源: 題型:
【題目】甲乙兩個學校高三年級分別有1100人,1000人,為了了解兩個學校全體高三年級學生在該地區一模考試的數學成績情況,采用分層抽樣方法從兩個學校一共抽取了105名學生的數學成績,并作出了頻數分布統計表如下:

(1)計算![]() ,
,![]() 的值;
的值;
(2)若規定考試成績在![]() 為優秀,請根據樣本估計乙校數學成績的優秀率;
為優秀,請根據樣本估計乙校數學成績的優秀率;
(3)若規定考試成績在![]() 內為優秀,由以上統計數據填寫下面
內為優秀,由以上統計數據填寫下面![]() 列聯表,若按是否優秀來判斷,是否有
列聯表,若按是否優秀來判斷,是否有![]() 的把握認為兩個學校的數學成績有差異.
的把握認為兩個學校的數學成績有差異.

附: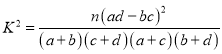 ,
,![]() .
.
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)="xln" x–ax2+(2a–1)x,a![]() R.
R.
(Ⅰ)令g(x)=f'(x),求g(x)的單調區間;
(Ⅱ)已知f(x)在x=1處取得極大值.求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】今年3月5日,國務院總理李克強作的政府工作報告中,提到要“懲戒學術不端,力戒學術不端,力戒浮躁之風”.教育部日前公布的《教育部2019年部門預算》中透露,2019年教育部擬抽檢博士學位論文約6000篇,預算為800萬元.國務院學位委員會、教育部2014年印發的《博士碩士學位論文抽檢辦法》通知中規定:每篇抽檢的學位論文送3位同行專家進行評議,3位專家中有2位以上(含2位)專家評議意見為“不合格”的學位論文,將認定為“存在問題學位論文”.有且只有1位專家評議意見為“不合格”的學位論文,將再送2位同行專家進得復評,2位復評專家中有1位以上(含1位)專家評議意見為“不合格”的學位論文,將認定為“存在問題學位論文”.設每篇學位論文被每位專家評議為“不合格”的概率均為![]() ,且各篇學位論文是否被評議為“不合格”相互獨立.
,且各篇學位論文是否被評議為“不合格”相互獨立.
(1)記一篇抽檢的學位論文被認定為“存在問題學位論文”的概率為![]() ,求
,求![]() ;
;
(2)若擬定每篇抽檢論文不需要復評的評審費用為900元,需要復評的評審費用為1500元;除評審費外,其它費用總計為100萬元.現以此方案實施,且抽檢論文為6000篇,問是否會超過預算?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了弘揚中華民族傳統文化,某中學高二年級舉行了“愛我中華,傳誦經典”的考試,并從中隨機抽取了![]() 名學生的成績(滿分
名學生的成績(滿分![]() 分)作為樣本,其中成績不低于
分)作為樣本,其中成績不低于![]() 分的學生被評為優秀生,得到成績分布的頻率分布直方圖如圖所示.
分的學生被評為優秀生,得到成績分布的頻率分布直方圖如圖所示.
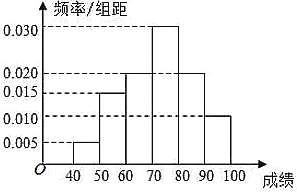
(1)若該年級共有![]() 名學生,試利用樣本估計該年級這次考試中優秀生人數;
名學生,試利用樣本估計該年級這次考試中優秀生人數;
(2)試估計這次參加考試的學生的平均成績(同一組數據用該組區間中點值作代表);
(3)若在樣本中,利用分層抽樣從成績不低于![]() 分的學生中隨機抽取
分的學生中隨機抽取![]() 人,再從中抽取
人,再從中抽取![]() 人贈送一套國學經典典籍,試求恰好抽中
人贈送一套國學經典典籍,試求恰好抽中![]() 名優秀生的概率.
名優秀生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】北京市政府為做好![]() 會議接待服務工作,對可能遭受污染的某海產品在進入餐飲區前必須進行兩輪檢測,只有兩輪都合格才能進行銷售,否則不能銷售.已知該海產品第一輪檢測不合格的概率為
會議接待服務工作,對可能遭受污染的某海產品在進入餐飲區前必須進行兩輪檢測,只有兩輪都合格才能進行銷售,否則不能銷售.已知該海產品第一輪檢測不合格的概率為![]() ,第二輪檢測不合格的概率為
,第二輪檢測不合格的概率為![]() ,兩輪檢測是否合格相互沒有影響.
,兩輪檢測是否合格相互沒有影響.
(1)求該海產品不能銷售的概率.
(2)如果該海產品可以銷售,則每件產品可獲利40元;如果該海產品不能銷售,則每件產品虧損80元(即獲利-80元).已知一箱中有該海產品4件,記一箱該海產品獲利![]() 元,求
元,求![]() 的分布列,并求出數學期望
的分布列,并求出數學期望![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com