【題目】某公司計劃在報刊與網絡媒體上共投放30萬元的廣告費，根據計劃，報刊與網絡媒體至少要投資4萬元．根據市場前期調研可知，在報刊上投放廣告的收益
與廣告費
滿足
，在網絡媒體上投放廣告的收益
與廣告費滿足
，設在報刊上投放的廣告費為(單位：萬元)，總收益為
(單位：萬元).
(1)當在報刊上投放的廣告費是18萬元時，求此時公司總收益；
(2)試問如何安排報刊、網絡媒體的廣告投資費，才能使總收益最大?
【答案】（1）16萬元；（2）當在報刊上投放的8萬元廣告費，在網絡媒體上投放22萬元廣告費時，總收益最大，且最大總收益為17萬元．
【解析】
（1）根據題意收益分為兩部分，報刊廣告收益和網絡媒體廣告收益，代入具體數值即可求解；
（2）列出總收益對應的表達式
，再利用換元法結合二次函數即可求得收益最大值
(1)當
時，此時在網絡媒體上的投資為12萬元，
所以總收益
(萬元).
(2)由題知，在報刊上投放的廣告費為
萬元，則在網絡媒體上投放廣告費為
萬元，
依題意得
，解得
，
所以
，
令
，則
，所以
=
.
當
，即
萬元時，
的最大值為17萬元．
所以，當在報刊上投放的8萬元廣告費，在網絡媒體上投放22萬元廣告費時，總收益最大，且最大總收益為17萬元．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】如果存在函數
（
為常數），使得對函數
定義域內任意
都有
成立，那么稱
為函數的一個“線性覆蓋函數”．給出如下四個結論：
①函數
存在“線性覆蓋函數”；
②對于給定的函數，其“線性覆蓋函數”可能不存在，也可能有無數個；
③
為函數
的一個“線性覆蓋函數”；
④若
為函數
的一個“線性覆蓋函數”，則
其中所有正確結論的序號是___________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
上任意一點到兩焦點
距離之和為
，離心率為
．
（1）求橢圓的標準方程；
（2）若直線
的斜率為
，直線
與橢圓C交于
兩點．點
為橢圓上一點，求
的面積的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某地有一企業2007年建廠并開始投資生產，年份代號為7，2008年年份代號為8，依次類推.經連續統計9年的收入情況如下表（經數據分析可用線性回歸模型擬合
與
的關系）：
年份代號（ | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
當年收入（ | 13 | 14 | 18 | 20 | 21 | 22 | 24 | 28 | 29 |
（Ⅰ）求
關于
的線性回歸方程
；
（Ⅱ）試預測2020年該企業的收入.
（參考公式：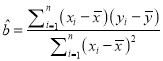 
， 
）
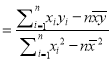查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在△OAB中，頂點A的坐標是(3，0)，頂點B的坐標是(1，2)，記△OAB位于直線
左側圖形的面積為f(t)．
（1）求函數f(t)的解析式；
（2）設函數
，求函數
的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
：
與直線
：
，動直線
過定點
.
（1）若直線與圓相切，求直線的方程；
（2）若直線與圓相交于
、
兩點，點M是PQ的中點，直線與直線相交于點N．探索
是否為定值，若是，求出該定值；若不是，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
；
（1）討論
的極值點的個數；
（2）若
，且
恒成立，求的最大值．
參考數據：
| 1.6 | 1.7 | 1.8 |
| 4.953 | 5.474 | 6.050 |
| 0.470 | 0.531 | 0.588 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題滿分12分，（1）小問5分，（2）小問7分）
如圖，橢圓
的左、右焦點分別為
過
的直線交橢圓于
兩點，且
（1）若
，求橢圓的標準方程
（2）若
求橢圓的離心率
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
