Question

求：(1)過A(2,)且平行于極軸的直線；(2)過A(3,)且和極軸成的直線.

Answer 1

思路分析：(1)在直線上任意取一點M，根據已知條件想辦法找到變量ρ、θ之間的關系.可以通過圖中的直角三角形來解決，因為已知OA的長度，還知∠AOx=，還可以得到MH的長度，從而在Rt△OMH中找到變量ρ、θ之間的關系.

(2)在三角形中利用正弦定理來找到變量ρ、θ之間的關系.

解：(1)如圖1-3-1所示,在直線l上任意取點M(ρ,θ)，∵A(2,)，

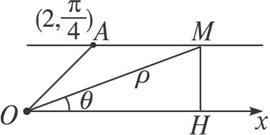
圖1-3-1

∴|MH|=2·sin=.在Rt△OMH中,|MH|=|OM|sinθ,即ρsinθ=,

∴過A(2,)平行于極軸的直線方程為ρsinθ=.

(2)如圖1-3-2所示,A(3,)，|OA|=3,∠AOB=，由已知∠MBx=，

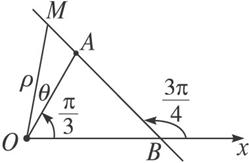
圖1-3-2

∴∠OAB=-=.

∴∠OAM=π-.

又∠OMA=∠MBx-θ=-θ.在△MOA中，

根據正弦定理得，

∵sin=sin(+)=，

將sin(-θ)展開，化簡上面的方程，可得ρ(sinθ+cosθ)=.

∴過A(3,)且和極軸成的直線為ρ(sinθ+cosθ)=.

    深化升華 可以看到，在求曲線方程時，要找出曲線上的點滿足的幾何條件，將它用坐標表示，再通過代數變換進行化簡.