
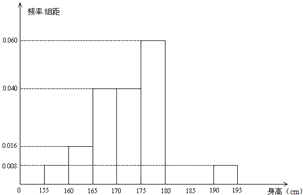
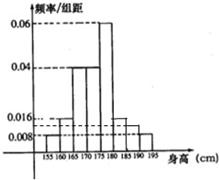
 解:(1)由頻率分布直方圖知,前五組頻率為(0.008+0.016+0.04+0.04+0.06)×5=0.82,
解:(1)由頻率分布直方圖知,前五組頻率為(0.008+0.016+0.04+0.04+0.06)×5=0.82,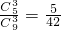 ,P(x=1)=
,P(x=1)= ,
,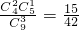 ,P(x=0)=
,P(x=0)=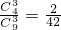 ,
,| X | 0 | 1 | 2 | 3 |
| P |  | 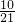 | 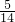 | 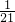 |
 …(12分)
…(12分)

 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:高中數學 來源: 題型:
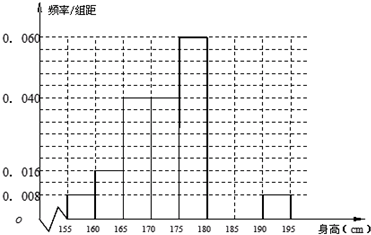
 從某學校高三年級共800名男生中隨機抽取50名測量身高,測量發現被測學生身高全部介于155cm和195cm之間,將測量結果按如下方式分成八組:第一組[155,160)、第二組[160,165);…第八組[190,195],右圖是按上述分組方法得到的頻率分布直方圖的一部分,已知第一組與第八組人數相同,第六組、第七組、第八組人數依次構成等差數列.
從某學校高三年級共800名男生中隨機抽取50名測量身高,測量發現被測學生身高全部介于155cm和195cm之間,將測量結果按如下方式分成八組:第一組[155,160)、第二組[160,165);…第八組[190,195],右圖是按上述分組方法得到的頻率分布直方圖的一部分,已知第一組與第八組人數相同,第六組、第七組、第八組人數依次構成等差數列.查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2012•咸陽三模)從某學校高三年級共800名男生中隨機抽取50人測量身高. 據測量,被測學生身高全部介于155cm到195cm之間,將測量結果按如下方式分成八組:第一組[155,160);第二組[160,165);…;第八組[190,195).
(2012•咸陽三模)從某學校高三年級共800名男生中隨機抽取50人測量身高. 據測量,被測學生身高全部介于155cm到195cm之間,將測量結果按如下方式分成八組:第一組[155,160);第二組[160,165);…;第八組[190,195).查看答案和解析>>
科目:高中數學 來源: 題型:

查看答案和解析>>
科目:高中數學 來源: 題型:
 從某學校高三年級共800名男生中隨機抽取50名測量身高,據測量被測學生身高全部介于155cm和195cm之間,將測量結果按如下方式分成八組;第一組[155,160)、第二組[160,165);…第八組[190,195),如圖是按上述分組方法得到的頻率分布直方圖的一部分,已知第一組與第八組人數相同,第六組、第七組、第八組人數依次構成等差數列.
從某學校高三年級共800名男生中隨機抽取50名測量身高,據測量被測學生身高全部介于155cm和195cm之間,將測量結果按如下方式分成八組;第一組[155,160)、第二組[160,165);…第八組[190,195),如圖是按上述分組方法得到的頻率分布直方圖的一部分,已知第一組與第八組人數相同,第六組、第七組、第八組人數依次構成等差數列.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com