
【題目】一次考試中,五位學生的數學,物理成績如下表所示:

(1)要從5名學生中選2人參加一項活動,求選中的學生中至少有一人的物理成績高于90分的概率;

(2)根據上表數據,畫出散點圖并用散點圖說明物理成績![]() 與數學成績
與數學成績![]() 之間線性相關關系的強弱,如果具有較強的線性相關關系,求
之間線性相關關系的強弱,如果具有較強的線性相關關系,求![]() 與
與![]() 的線性回歸方程(系數精確到0.01);如果不具有線性相關關系,請說明理由.
的線性回歸方程(系數精確到0.01);如果不具有線性相關關系,請說明理由.
參考公式:
回歸直線的方程是![]() ,其中
,其中 ,
, ![]() ,
,
![]() 是與
是與![]() 對應的回歸估計值,
對應的回歸估計值,
參考數據: ![]() ,
, ![]() .
.
【答案】(1) ![]() ;(2)答案見解析.
;(2)答案見解析.
【解析】試題分析:
(1)由題意列出所有可能的事件,結合古典概型計算公式可得至少有一人的物理成績高于90分的概率為![]() ;
;
(2)繪制散點圖,觀察可得物理成績與數學成績高度正相關.結合線性回歸方程的計算公式可得:線性回歸方程為![]() .
.
試題解析:
(1)從5名學生中任取2名學生的所有情況為:(A1,A2),(A1,A3),(A1,A4),(A1,A5),(A2,A3),(A2,A4),(A2,A5),(A3,A4),(A3,A5),(A4,A5),共10種情況.
其中至少有一人的物理成績高于90分的情況有:
(A1,A2),(A1,A4),(A2,A3),(A2,A4),(A2,A5),(A3,A4),(A4,A5)共7種情況,
故選中的學生中至少有一人的物理成績高于90分的概率為![]() .
.
(2)
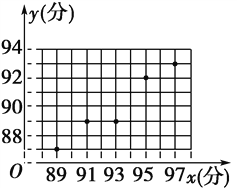
可以看出,物理成績與數學成績高度正相關.散點圖如圖所示:
從散點圖可以看出這些點大致分布在一條直線附近,并且在逐步上升,故物理成績與數學成績正相關.
設y與x的線性回歸方程是![]() =
=![]() x+
x+![]() ,根據所給的數據,可以計算出
,根據所給的數據,可以計算出
![]() =93,
=93,![]() =90,
=90,
![]() =
=![]() =0.75,
=0.75,![]() =90-0.75×93=20.25,
=90-0.75×93=20.25,
所以y與x的線性回歸方程是
![]() =0.75x+20.25.
=0.75x+20.25.


 智能訓練練測考系列答案
智能訓練練測考系列答案科目:高中數學 來源: 題型:
【題目】如圖,為迎接校慶,我校準備在直角三角形ABC內的空地上植造一塊“綠地△ABD”,規劃在△ABD的內接正方形BEFG內種花,其余地方種草,若AB=a,∠DAB=θ,種草的面積為S1 , 種花的面積為S2 , 比值 ![]() 稱為“規劃和諧度”.
稱為“規劃和諧度”.
(1)試用a,θ表示S1 , S2;
(2)若a為定值,BC足夠長,當θ為何值時,“規劃和諧度”有最小值,最小值是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某石化集團獲得了某地深海油田區塊的開發權,集團在該地區隨機初步勘探了部分幾口井,取得了地質資料,進入全面勘探時期后,集團按網絡點來布置井位進行全面勘探,由于勘探一口井的費用很高,如果新設計的井位與原有井位重合或接近,便利用舊井的地質資料,不必打這口新井,以節約勘探費用,勘探初期數據資料見如表:

(參考公式和計算結果:  ,
, ![]() ,
, ![]() ,
, ![]() )
)
(1)1~6號井位置線性分布,借助前5組數據(坐標![]() )求得回歸直線方程為
)求得回歸直線方程為![]() ,求
,求![]() 的值,并估計
的值,并估計![]() 的預報值;
的預報值;
(2)現準備勘探新井![]() ,若通過1,3,5,7號并計算出的(
,若通過1,3,5,7號并計算出的(![]() ,
, ![]() 精確到0.01),設
精確到0.01),設 ,
,  ,當
,當![]() 均不超過10%時,使用位置最接近的已有舊井
均不超過10%時,使用位置最接近的已有舊井![]() ,否則在新位置打開,請判斷可否使用舊井?
,否則在新位置打開,請判斷可否使用舊井?
(3)設出油量與勘探深度的比值![]() 不低于20的勘探井稱為優質井,那么在原有6口井中任意勘探4口井,求勘探優質井數
不低于20的勘探井稱為優質井,那么在原有6口井中任意勘探4口井,求勘探優質井數![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C所對的邊分別為a,b,c,且 ![]() asinA=(
asinA=( ![]() b﹣c)sinB+(
b﹣c)sinB+( ![]() c﹣b)sinC.
c﹣b)sinC.
(1)求角A的大小;
(2)若a= ![]() ,cosB=
,cosB= ![]() ,D為AC的中點,求BD的長.
,D為AC的中點,求BD的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于平面向量 ![]() ,
, ![]() ,
, ![]() ,下列結論正確的個數為( ) ①若
,下列結論正確的個數為( ) ①若 ![]()
![]() =
= ![]()
![]() ,則
,則 ![]() =
= ![]() ;
;
②若 ![]() =(1,k),
=(1,k), ![]() =(﹣2,6),
=(﹣2,6), ![]() ∥
∥ ![]() ,則k=﹣3;
,則k=﹣3;
③非零向量 ![]() 和
和 ![]() 滿足|
滿足| ![]() |=|
|=| ![]() |=|
|=| ![]() ﹣
﹣ ![]() |,則
|,則 ![]() 與
與 ![]() +
+ ![]() 的夾角為30°;
的夾角為30°;
④已知向量 ![]() ,且
,且 ![]() 與
與 ![]() 的夾角為銳角,則實數λ的取值范圍是
的夾角為銳角,則實數λ的取值范圍是 ![]() .
.
A.4個
B.3個
C.2個
D.1個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=asinxcosx﹣ ![]() acos2x+
acos2x+ ![]() a+b(a>0)
a+b(a>0)
(1)寫出函數的單調遞減區間;
(2)設x∈[0, ![]() ],f(x)的最小值是﹣2,最大值是
],f(x)的最小值是﹣2,最大值是 ![]() ,求實數a,b的值.
,求實數a,b的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足a2= ![]() ,且an+1=3an﹣1(n∈N*).
,且an+1=3an﹣1(n∈N*).
(1)求數列{an}的通項公式以及數列{an}的前n項和Sn的表達式;
(2)若不等式 ![]() ≤m對n∈N*恒成立,求實數m的取值范圍.
≤m對n∈N*恒成立,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com