
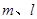 ,平面
,平面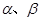 ,且
,且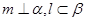 ,給出下列命題:
,給出下列命題: 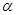 ∥
∥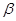 ,則m⊥
,則m⊥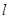 ; ②若
; ②若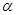 ⊥
⊥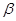 ,則m∥
,則m∥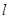 ;
;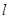 ,則
,則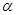 ∥
∥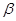 ; ④若m∥
; ④若m∥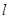 ,則
,則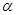 ⊥
⊥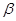 .其中正確命題的個數(shù)是( )
.其中正確命題的個數(shù)是( )| A.1 | B.2 | C.3 | D.4 |
科目:高中數(shù)學 來源:不詳 題型:解答題

查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
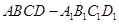 中
中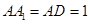 ,
,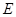 為
為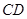 中點.
中點.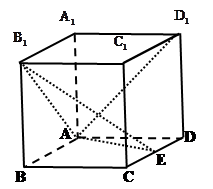
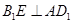 ;
;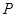 ,使得
,使得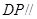 平面
平面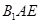 ?若存在,求
?若存在,求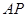 的長;若不存在,說明理由;
的長;若不存在,說明理由;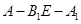 的大小為
的大小為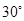 ,求
,求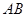 的長.
的長.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:填空題
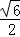
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
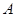 作平面
作平面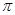 的垂線,垂足為
的垂線,垂足為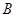 ,記
,記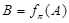 .設(shè)
.設(shè)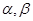 是兩個不同的平面,對空間任意一點
是兩個不同的平面,對空間任意一點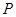 ,
,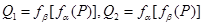 ,恒有
,恒有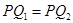 ,則( )
,則( )A.平面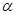 與平面 與平面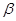 垂直 垂直 | B.平面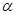 與平面 與平面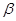 所成的(銳)二面角為 所成的(銳)二面角為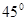 |
C.平面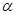 與平面 與平面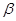 平行 平行 | D.平面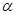 與平面 與平面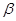 所成的(銳)二面角為 所成的(銳)二面角為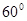 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:填空題
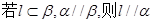 ②
②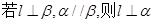
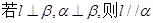 ④
④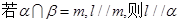
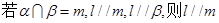
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com