(本小題滿分12分) 已知
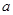
為實數(shù),
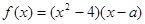
,
(Ⅰ)若a=2,求
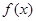
的單調遞增區(qū)間;
(Ⅱ)若
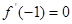
,求
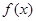
在[-2,2] 上的最大值和最小值。
試題分析:(Ⅰ)由
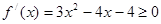
,得
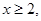
或

所以當a=2時f(x)的單調遞增區(qū)間為

或
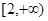
(6分)
(Ⅱ)由原式得
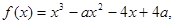
∴
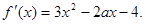
由

得
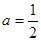
,此時有
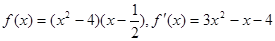
.
令

得
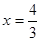
或x="-1" , 又
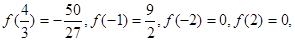
所以f(x)在[-2,2]上的最大值為
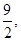
最小值為
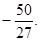
(12分)
點評:利用函數(shù)的導數(shù)可以求單調區(qū)間,極值,最值等問題
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:單選題
函數(shù)
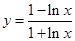
的導數(shù)是 ( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
若曲線
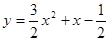
的某一切線與直線
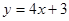
平行,則切點坐標
為
,切線方程為
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分15分)過曲線C:
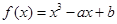
外的點A(1,0)作曲線C的切線恰有兩條,
(Ⅰ)求
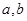
滿足的等量關系;
(Ⅱ)若存在
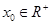
,使

成立,求

的取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知雙曲線
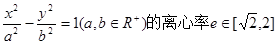
,則一條漸近線與實軸所構成的角的取值范圍是
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
設函數(shù)
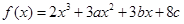
在

及

時取得極值.
(I)求

的值;
(II)若對于任意的
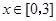
,都有
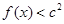
成立,求c的取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
如圖,函數(shù)

的圖象是折線段
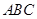
,其中

的坐標分別為
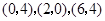
, 函數(shù)

在
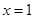
處的導數(shù)
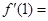
________.

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
曲線
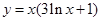
在點
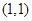
處的切線方程為__________________ .
查看答案和解析>>

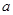 為實數(shù),
為實數(shù),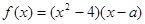 ,
,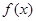 的單調遞增區(qū)間;
的單調遞增區(qū)間;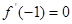 ,求
,求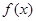 在[-2,2] 上的最大值和最小值。
在[-2,2] 上的最大值和最小值。 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案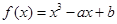 外的點A(1,0)作曲線C的切線恰有兩條,
外的點A(1,0)作曲線C的切線恰有兩條,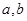 滿足的等量關系;
滿足的等量關系;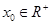 ,使
,使 成立,求
成立,求 的取值范圍.
的取值范圍.