
【題目】下表提供了某廠節能降耗技術改造后生產甲產品過程中記錄的產量x(噸)與相應的生產能耗y(噸標準煤)的幾組對照數據.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(參考數值:3×2.5+4×3+5×4+6×4.5=66.5)
(1)請畫出上表數據的散點圖;
(2)請根據上表提供的數據,用最小二乘法求出y關于x的線性回歸方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(3)已知該廠技改前100噸甲產品的生產能耗為90噸標準煤.試根據第2題求出的回歸方程,預測生產100噸甲產品的生產能耗比技改前降低多少噸標準煤?
【答案】
(1)解:把所給的四對數據寫成對應的點的坐標,
在坐標系中描出來,得到散點圖如下;
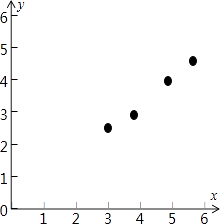
(2)解:由對照數據,計算得
![]() =
= ![]() ×(3+4+5+6)=4.5,
×(3+4+5+6)=4.5,
![]() =
= ![]() ×(2.5+3+4+4.5)=3.5,
×(2.5+3+4+4.5)=3.5,
![]() =32+42+52+62=86,
=32+42+52+62=86,
![]() xiyi=3×2.5+4×3+5×4+6×4.5=66.5,
xiyi=3×2.5+4×3+5×4+6×4.5=66.5,
∴回歸方程的系數為 ![]() =
= ![]() =0.7,
=0.7,
![]() =3.5﹣0.7×4.5=0.35,
=3.5﹣0.7×4.5=0.35,
∴所求線性回歸方程為 ![]() =0.7x+0.35
=0.7x+0.35
(3)解:由(2)的線性回歸方程,估計生產100噸甲產品的生產能耗為
0.7×100+0.35=70.35(噸),
∴90﹣70.35=19.65噸,
預測比技改前降低了19.65噸標準煤
【解析】(1)把所給的四對數據寫成對應的點的坐標,在坐標系中描出來,得到散點圖;(2)根據所給的這組數據求出回歸方程的系數,得到線性回歸方程;(3)根據線性回歸方程,計算x=100時的生產能耗,求出比技改前降低的標準煤.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() x2﹣alnx(a∈R)
x2﹣alnx(a∈R)
(1)若函數f(x)在x=2處的切線方程為y=x+b,求a,b的值;
(2)討論方程f(x)=0解的個數,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數g(x)=ax2-2ax+1+b(a>0)在區間[2,4]上的最大值為9,最小值為1,記f(x)=g(|x|)。
(1)求實數a,b的值;
(2)若不等式f(2k)>1成立,求實數k的取值范圍;
(3)定義在[p,q]上的函數![]() (x),設p=x0<x1<…<xi-1<xi<…<xn=q,x1,x2,…,xn-l將區間[p,q]任意劃分成n個小區間,如果存在一個常數M>0,使得和式
(x),設p=x0<x1<…<xi-1<xi<…<xn=q,x1,x2,…,xn-l將區間[p,q]任意劃分成n個小區間,如果存在一個常數M>0,使得和式![]() 恒成立,則稱函數
恒成立,則稱函數![]() (x)為在[p,q]上的有界變差函數。試判斷函數f(x)是否為在[0,4]上的有界變差函數?若是,求M的最小值;若不是,請說明理由。
(x)為在[p,q]上的有界變差函數。試判斷函數f(x)是否為在[0,4]上的有界變差函數?若是,求M的最小值;若不是,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國有個名句“運籌帷幄之中,決勝千里之外.”其中的“籌”原意是指《孫子算經》中記載的算籌,古代是用算籌來進行計算,算籌是將幾寸長的小竹棍擺在平面上進行運算,算籌的擺放形式有縱橫兩種形式,如表 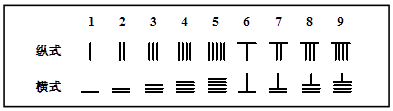
表示一個多位數時,像阿拉伯計數一樣,把各個數位的數碼從左到右排列,但各位數碼的籌式需要縱橫相間,個位,百位,萬位數用縱式表示,十位,千位,十萬位用橫式表示,以此類推,例如6613用算籌表示就是: ![]() ,則9117用算籌可表示為( )
,則9117用算籌可表示為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy 中,已知圓C的參數方程為 ![]() (φ為參數).以坐標原點為極點,x軸正半軸為極軸建立極坐標系.
(φ為參數).以坐標原點為極點,x軸正半軸為極軸建立極坐標系.
(1)求圓的極坐標方程;
(2)直線l的極坐方程是 ![]() ,射線OM:θ=
,射線OM:θ= ![]() 與圓的交點為O,P,與直線l的交點為Q,求線段PQ的長.
與圓的交點為O,P,與直線l的交點為Q,求線段PQ的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市居民自來水收費標準如下:每戶每月用水不超過4噸時,每噸為1.80元,當用水超過4噸時,超過部分每噸3.00元.某月甲、乙兩戶共交水費y元,已知甲、乙兩用戶該月用水量分別為5x,3x噸. (Ⅰ) 若x=1,求該月甲、乙兩戶的水費;
(Ⅱ) 求y關于x的函數;
(Ⅲ) 若甲、乙兩戶該月共交水費26.4元,分別求出甲、乙兩戶該月的用水量.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正三棱柱ABCA1B1C1中,AB=2,AA1=3,
D為C1B的中點,P為AB邊上的動點.
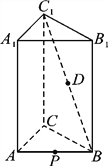
(1)當點P為AB的中點時,證明DP∥平面ACC1A1;
(2)若AP=3PB,求三棱錐BCDP的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在二項式( ![]() +
+ ![]() )n展開式中,前三項的系數成等差數列. 求:(1)展開式中各項系數和;
)n展開式中,前三項的系數成等差數列. 求:(1)展開式中各項系數和;
【答案】解:由題意得2 ![]() ×
× ![]() =1+
=1+ ![]() ×
× ![]() ,
,
化為:n2﹣9n+8=0,解得n=1(舍去)或8.
∴n=8.
在 ![]() 中,令x=1,可得展開式中各項系數和=
中,令x=1,可得展開式中各項系數和= ![]() =
= ![]() .
.
(1)展開式中系數最大的項.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com