
【題目】在直角坐標系xOy 中,已知圓C的參數方程為 ![]() (φ為參數).以坐標原點為極點,x軸正半軸為極軸建立極坐標系.
(φ為參數).以坐標原點為極點,x軸正半軸為極軸建立極坐標系.
(1)求圓的極坐標方程;
(2)直線l的極坐方程是 ![]() ,射線OM:θ=
,射線OM:θ= ![]() 與圓的交點為O,P,與直線l的交點為Q,求線段PQ的長.
與圓的交點為O,P,與直線l的交點為Q,求線段PQ的長.
【答案】
(1)解:圓C的參數方程為 ![]() (φ為參數).
(φ為參數).
消去參數可得:(x﹣1)2+y2=1.
把x=ρcosθ,y=ρsinθ代入化簡得此圓的極坐標方程為:ρ=2cosθ
(2)解:如圖所示,直線l的極坐方程是 ![]() ,
,
射線OM:θ= ![]() .
.
可得普通方程:直線l:y+ ![]() x=3
x=3 ![]() ,射線OM:y=
,射線OM:y= ![]() x.
x.
聯立 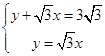 ,解得x=
,解得x= ![]() ,y=
,y= ![]() ,即Q(
,即Q( ![]() ).
).
聯立  ,解得
,解得 ![]() 或
或 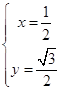 .
.
∴P( ![]() ,
, ![]() ).
).
∴|PQ|= ![]() =2.
=2.
∴線段PQ的長為2
【解析】(1)圓C的參數方程消去參數能求出圓的極坐標方程,把x=ρcosθ,y=ρsinθ代入化簡能求出此圓的極坐標方程.(II)求出直線l:y+ ![]() x=3
x=3 ![]() ,射線OM:y=
,射線OM:y= ![]() x.聯立
x.聯立 ![]() ,得Q(
,得Q( ![]() ),聯立
),聯立 ![]() ,得P(
,得P( ![]() ,
, ![]() ),由此能求出線段PQ的長.
),由此能求出線段PQ的長.


 黃岡小狀元解決問題天天練系列答案
黃岡小狀元解決問題天天練系列答案 三點一測快樂周計劃系列答案
三點一測快樂周計劃系列答案科目:高中數學 來源: 題型:
【題目】某食品的保鮮時間t(單位:小時)與儲藏溫度x(單位:℃)滿足函數關系t=![]() 且該食品在4℃的保鮮時間是16小時。已知甲在某日上午10時購買了該食品,并將其遺放在室外,且此日的室外溫度隨時間變化如圖所示。給出以下四個結論:
且該食品在4℃的保鮮時間是16小時。已知甲在某日上午10時購買了該食品,并將其遺放在室外,且此日的室外溫度隨時間變化如圖所示。給出以下四個結論: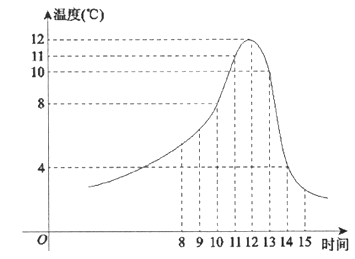
①該食品在6℃的保鮮時間是8小時;
②當x∈[-6,6]時,該食品的保鮮時間t隨著x增大而逐漸減少;
③到了此日13時,甲所購買的食品還在保鮮時間內;
④到了此日14時,甲所購買的食品已然過了保鮮時間。
其中,所有正確結論的序號是__________。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設y=f(x)是二次函數,方程f(x)=0有兩個相等的實根,且f′(x)=2x+2.
(1)求y=f(x)的表達式;
(2)求y=f(x)的圖象與兩坐標軸所圍成封閉圖形的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a>0,設p:實數x滿足x2﹣4ax+3a2<0,q:實數x滿足(x﹣3)2<1.
(1)若a=1,且p∧q為真,求實數x的取值范圍;
(2)若¬p是¬q的充分不必要條件,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表提供了某廠節能降耗技術改造后生產甲產品過程中記錄的產量x(噸)與相應的生產能耗y(噸標準煤)的幾組對照數據.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(參考數值:3×2.5+4×3+5×4+6×4.5=66.5)
(1)請畫出上表數據的散點圖;
(2)請根據上表提供的數據,用最小二乘法求出y關于x的線性回歸方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(3)已知該廠技改前100噸甲產品的生產能耗為90噸標準煤.試根據第2題求出的回歸方程,預測生產100噸甲產品的生產能耗比技改前降低多少噸標準煤?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數![]() 的圖象經過點
的圖象經過點![]() ,且函數
,且函數![]() =
= ![]() 是偶函數
是偶函數
(1)求![]() 的解析式;
的解析式;
(2)已知![]() ,求函數
,求函數![]() 在
在![]() 的最大值和最小值
的最大值和最小值
(3)函數![]() 的圖象上是否存在這樣的點,其橫坐標是正整數,縱坐標是一個完全平方數?如果存在,求出這樣的點的坐標;如果不存在,請說明理由.
的圖象上是否存在這樣的點,其橫坐標是正整數,縱坐標是一個完全平方數?如果存在,求出這樣的點的坐標;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分別為CD和PC的中點.

求證:(1) BE∥平面PAD;
(2) 平面BEF⊥平面PCD.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com