
【題目】已知x0,x0+![]() 是函數(shù)f(x)=cos2(wx﹣
是函數(shù)f(x)=cos2(wx﹣![]() )﹣sin2wx(ω>0)的兩個(gè)相鄰的零點(diǎn)
)﹣sin2wx(ω>0)的兩個(gè)相鄰的零點(diǎn)
(1)求![]() 的值;
的值;
(2)若對任意![]() ,都有f(x)﹣m≤0,求實(shí)數(shù)m的取值范圍.
,都有f(x)﹣m≤0,求實(shí)數(shù)m的取值范圍.
(3)若關(guān)于![]() 的方程
的方程![]() 在
在![]() 上有兩個(gè)不同的解,求實(shí)數(shù)
上有兩個(gè)不同的解,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】試題分析:(1)利用三角恒等變形,對原函數(shù)進(jìn)行化簡變形,可得![]() ,由兩相鄰零點(diǎn)可得函數(shù)最小正周期,再利用最小正周期與
,由兩相鄰零點(diǎn)可得函數(shù)最小正周期,再利用最小正周期與![]() 的關(guān)系可得函數(shù)表達(dá)式,將
的關(guān)系可得函數(shù)表達(dá)式,將![]() 代入可得其值;(2)實(shí)數(shù)
代入可得其值;(2)實(shí)數(shù)![]() 的取值范圍可轉(zhuǎn)化為求函數(shù)
的取值范圍可轉(zhuǎn)化為求函數(shù)![]() 在
在![]() 的最大值問題,利用三角函數(shù)的性質(zhì)可得結(jié)果;(3)類比第二小題,利用分離變量求出
的最大值問題,利用三角函數(shù)的性質(zhì)可得結(jié)果;(3)類比第二小題,利用分離變量求出![]() 的取值范圍,結(jié)合圖象可知與
的取值范圍,結(jié)合圖象可知與![]() 有兩交點(diǎn)時(shí)
有兩交點(diǎn)時(shí)![]() 的范圍.
的范圍.
試題解析:(1)f(x)=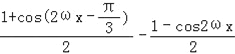 =
=![]()
=![]() =
=![]()
=![]() (
(![]() )=
)=![]() .
.
由題意可知,f(x)的最小正周期T=π,
∴![]() , 又∵ω>0, ∴ω=1,
, 又∵ω>0, ∴ω=1,
∴f(x)=![]() .
.
∴![]() =
=![]() .
.
(2)由f(x)﹣m≤0得,f(x)≤m, ∴m≥f(x)max,
∵﹣![]() , ∴
, ∴![]() , ∴
, ∴![]() ,
,
∴﹣![]() ≤
≤![]() , 即f(x)max=
, 即f(x)max=![]() ,
,
∴![]() 所以
所以![]()
(3)原方程可化為![]()
即![]()
![]()
畫出![]()
![]() 的草圖
的草圖
x=0時(shí),y=2sin![]() =
=![]() ,
,
y的最大值為2,
∴要使方程在x∈[0, ![]() ]上有兩個(gè)不同的解,
]上有兩個(gè)不同的解,
即![]() ≤m+1<2, 即
≤m+1<2, 即![]() ﹣1≤m<1. 所以
﹣1≤m<1. 所以![]()


 黎明文化寒假作業(yè)系列答案
黎明文化寒假作業(yè)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,
,![]() .
.
(1)求當(dāng)![]() 時(shí),
時(shí),![]() 的值域;
的值域;
(2)若函數(shù)![]() 在
在![]() 內(nèi)有且只有一個(gè)零點(diǎn),求
內(nèi)有且只有一個(gè)零點(diǎn),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】直三棱柱ABC-A1B1C1中,AB=AA1,∠CAB=![]() .
.

(1)證明:CB1⊥BA1;
(2)已知AB=2,BC=![]() ,求三棱錐C1-ABA1的體積.
,求三棱錐C1-ABA1的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】我國是世界上嚴(yán)重缺水的國家之一,城市缺水問題較為突出,某市政府為了鼓勵(lì)居民節(jié)約用水,計(jì)劃調(diào)整居民生活用水收費(fèi)方案,擬確定一個(gè)合理的月用水量標(biāo)準(zhǔn)![]() (噸),一位居民的月用水量不超過
(噸),一位居民的月用水量不超過![]() 的部分按平價(jià)收費(fèi),超出
的部分按平價(jià)收費(fèi),超出![]() 的部分按議價(jià)收費(fèi),為了了解居民用水情況,通過抽祥,獲得了某年
的部分按議價(jià)收費(fèi),為了了解居民用水情況,通過抽祥,獲得了某年![]() 位居民毎人的月均用水量(單位:噸),將數(shù)據(jù)按照
位居民毎人的月均用水量(單位:噸),將數(shù)據(jù)按照![]() 分成
分成![]() 組,制成了如圖所示的頻率分布直方圖.
組,制成了如圖所示的頻率分布直方圖.
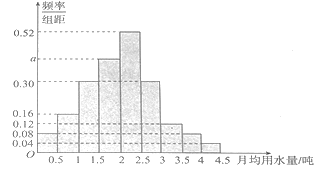
(1)求直方圖中![]() 的值;
的值;
(2)若該市有![]() 萬居民,估計(jì)全市居民中月均用水量不低于
萬居民,估計(jì)全市居民中月均用水量不低于![]() 噸的人數(shù),并說明理由;
噸的人數(shù),并說明理由;
(3)若該市政府希望使![]() 的居民每月的用水量不超過標(biāo)準(zhǔn)
的居民每月的用水量不超過標(biāo)準(zhǔn)![]() (噸),估計(jì)
(噸),估計(jì)![]() 的值(精確到
的值(精確到![]() ),并說明理由.
),并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
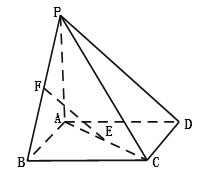
【題目】如圖,四棱錐![]() 的底面
的底面![]() 為正方形,
為正方形,![]() ⊥底面
⊥底面![]() ,
,![]() 分別是
分別是![]() 的中點(diǎn),
的中點(diǎn),![]() .
.
(Ⅰ)求證![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求直線![]() 與平面
與平面![]() 所成的角;
所成的角;
(Ⅲ)求四棱錐![]() 的外接球的體積.
的外接球的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 的焦點(diǎn)為
的焦點(diǎn)為![]() ,拋物線上橫坐標(biāo)為
,拋物線上橫坐標(biāo)為![]() 的點(diǎn)到拋物線頂點(diǎn)的距離與該點(diǎn)到拋物線準(zhǔn)線的距離相等。
的點(diǎn)到拋物線頂點(diǎn)的距離與該點(diǎn)到拋物線準(zhǔn)線的距離相等。
(1)求拋物線![]() 的方程;
的方程;
(2)設(shè)直線![]() 與拋物線
與拋物線![]() 交于
交于![]() 兩點(diǎn),若
兩點(diǎn),若![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的值。
的值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】三國魏人劉徽,自撰《海島算經(jīng)》,專論測高望遠(yuǎn).其中有一題:今有望海島,立兩表齊,高三丈,前後相去千步,令後表與前表相直。從前表卻行一百二十三步,人目著地取望島峰,與表末參合。從後表卻行百二十七步,人目著地取望島峰,亦與表末參合。問島高及去表各幾何?翻譯如下:要測量海島上一座山峰![]() 的高度
的高度![]() ,立兩根高三丈的標(biāo)桿
,立兩根高三丈的標(biāo)桿![]() 和
和![]() ,前后兩竿相距
,前后兩竿相距![]() 步,使后標(biāo)桿桿腳
步,使后標(biāo)桿桿腳![]() 與前標(biāo)桿桿腳
與前標(biāo)桿桿腳![]() 與山峰腳
與山峰腳![]() 在同一直線上,從前標(biāo)桿桿腳
在同一直線上,從前標(biāo)桿桿腳![]() 退行
退行![]() 步到
步到![]() ,人眼著地觀測到島峰,
,人眼著地觀測到島峰,![]() 、
、![]() 、
、![]() 、三點(diǎn)共線,從后標(biāo)桿桿腳
、三點(diǎn)共線,從后標(biāo)桿桿腳![]() 退行
退行![]() 步到
步到![]() ,人眼著地觀測到島峰,
,人眼著地觀測到島峰,![]() 、
、![]() 、
、![]() 三點(diǎn)也共線,則山峰的高度
三點(diǎn)也共線,則山峰的高度![]() __________步.(古制
__________步.(古制![]() 步
步![]() 尺,
尺,![]() 里
里![]() 丈
丈![]() 尺
尺![]() 步)
步)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若方程![]()
![]() 有兩個(gè)相異實(shí)根
有兩個(gè)相異實(shí)根![]() ,
,![]() ,且
,且![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com