
根據統計資料,某工藝品廠的日產量最多不超過20件,每日產品廢品率 與日產量
與日產量 (件)之間近似地滿足關系式
(件)之間近似地滿足關系式 (日產品廢品率
(日產品廢品率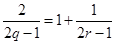
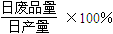 ).已知每生產一件正品可贏利2千元,而生產一件廢品則虧損1千元.(該車間的日利潤
).已知每生產一件正品可贏利2千元,而生產一件廢品則虧損1千元.(該車間的日利潤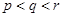 日正品贏利額
日正品贏利額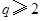 日廢品虧損額)
日廢品虧損額)
(1)將該車間日利潤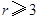 (千元)表示為日產量
(千元)表示為日產量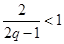 (件)的函數;
(件)的函數;
(2)當該車間的日產量為多少件時,日利潤最大?最大日利潤是幾千元?
(1)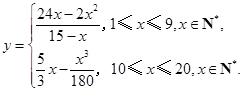 ,(2)日產量為10件時,日利潤最大,最大日利潤是
,(2)日產量為10件時,日利潤最大,最大日利潤是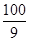 千元.
千元.
解析試題分析:(1)解實際問題應用題,關鍵正確理解題意,列出函數關系式. 日產量為 件時,廢品為
件時,廢品為 件,正品為
件,正品為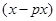 件,因此贏利
件,因此贏利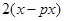 ,虧損
,虧損 ,利潤為
,利潤為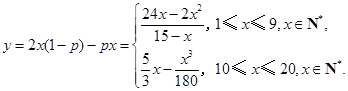 (2)求分段函數最值,需分別求. 當
(2)求分段函數最值,需分別求. 當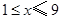 時,利用導數為零得
時,利用導數為零得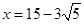 ,列表分析知當
,列表分析知當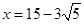 時,
時,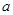 取得極大值,也是最大值,又
取得極大值,也是最大值,又 是整數,
是整數,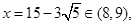
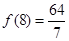 ,
,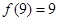 ,所以當
,所以當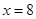 時,
時, 有最大值
有最大值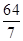 .當
.當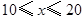 時,
時,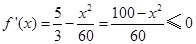 ,所以函數
,所以函數 在
在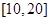 上單調減,所以當
上單調減,所以當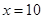 時,
時, 取得極大值
取得極大值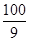 ,也是最大值.由于
,也是最大值.由于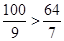 ,所以當該車間的日產量為10件時,日利潤最大.
,所以當該車間的日產量為10件時,日利潤最大.
試題解析:(1)由題意可知,

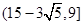
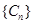
 4分
4分
(2)考慮函數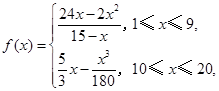
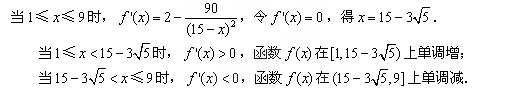
當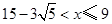 時,
時,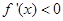 ,函數
,函數 在
在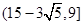 上單調減.
上單調減.
所以當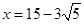 時,
時,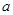 取得極大值,也是最大值,
取得極大值,也是最大值,
又 是整數,
是整數,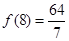 ,
,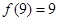 ,所以當
,所以當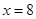 時,
時, 有最大值
有最大值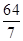 . 10分
. 10分
當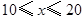 時,
時,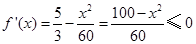 ,所以函數
,所以函數 在
在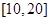 上單調減,
上單調減,
所以當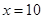 時,
時, 取得極大值
取得極大值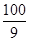 ,也是最大值.
,也是最大值.
由于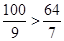 ,所以當該車間的日產量為10件時,日利潤最大.
,所以當該車間的日產量為10件時,日利潤最大.
答:當該車間的日產量為10件時,日利潤最大,最大日利潤是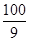 千元. 14分
千元. 14分
考點:函數解析式,利用導數求函數最值


科目:高中數學 來源: 題型:解答題
某公司經銷某種產品,每件產品的成本為6元,預計當每件產品的售價為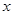 元(
元(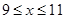 )時,一年的銷售量為
)時,一年的銷售量為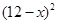 萬件。
萬件。
(1)求公司一年的利潤y(萬元)與每件產品的售價x的函數關系;
(2)當每件產品的售價為多少時,公司的一年的利潤y最大,求出y最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數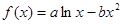 圖像上一點
圖像上一點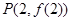 處的切線方程為
處的切線方程為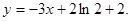 (1)求
(1)求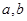 的值;(2)若方程
的值;(2)若方程 在區間
在區間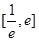 內有兩個不等實根,求
內有兩個不等實根,求 的取值范圍;(3)令
的取值范圍;(3)令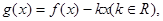 如果
如果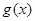 的圖像與
的圖像與 軸交于
軸交于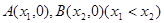 兩點,
兩點,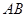 的中點為
的中點為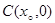 ,求證:
,求證: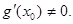
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com