
設 =(-3,m),
=(-3,m),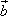 =(4,3),若
=(4,3),若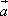 與
與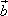 的夾角是鈍角,則實數m的取值范圍是
的夾角是鈍角,則實數m的取值范圍是
m≠4且m≠-![]()
m<4且m≠-![]()
m>4
m<4
 浙江新課程三維目標測評課時特訓系列答案
浙江新課程三維目標測評課時特訓系列答案 周周清檢測系列答案
周周清檢測系列答案 輕巧奪冠周測月考直通高考系列答案
輕巧奪冠周測月考直通高考系列答案科目:高中數學 來源:廣東省潮州金山中學2010-2011學年高二下學期期中考試數學文科試卷 題型:044
若實數m,n為關于x的一元二次方程Ax2+Bx+C=0的兩個實數根,則有Ax2+Bx+C=A(x-m)(x-n),由系數可得:m+n=-![]() ,且m·n=
,且m·n=![]() .設x1,x2,x3為關于x的方程f(x)=x3-ax2+bx-c=0,(a,b,c∈R)的三個實數根.
.設x1,x2,x3為關于x的方程f(x)=x3-ax2+bx-c=0,(a,b,c∈R)的三個實數根.
(1)寫出三次方程的根與系數的關系;即x1+x2+x3=_________;x1x2+x2x3+x3x1=_________;x1·x2·x3=_________
(2)若a,b,c均大于零,試證明:x1,x2,x3都大于零
(3)若a∈Z,b∈Z,|b|<2,f(x)在x=α,x=β處取得極值,且-1<α<β<1,求方程f(x)=0三個實根兩兩不相等時,實數c的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
設集合U={1,2,3,4},M={1,2,3},N={2,3,4},則∁U(M∩N)=( )
A.{1,2} B.{2,3}
C.{2,4} D.{1,4}
查看答案和解析>>
科目:高中數學 來源: 題型:
設函數f(x)=-![]() x3+x2+(m2-1)x(x∈R),其中m>0.
x3+x2+(m2-1)x(x∈R),其中m>0.
(1)當m=1時,求曲線y=f(x)在(1,f(1))點處的切線的方程;
(2)求函數f(x)的單調區間與極值;
(3)已知函數g(x)=f(x)+![]() 有三個互不相同的零點,求m的取值范圍.
有三個互不相同的零點,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年河北省高三8月月考理科數學試卷(解析版) 題型:解答題
已知函數f(x)=ax3+bx2+cx在x=±1處取得極值,且在x=0處的切線的斜率為-3.
(1)求f(x)的解析式;
(2)若過點A(2,m)可作曲線y=f(x)的三條切線,求實數m的取值范圍.
【解析】本試題主要考查了導數在研究函數中的運用。第一問,利用函數f(x)=ax3+bx2+cx在x=±1處取得極值,且在x=0處的切線的斜率為-3,得到c=-3 ∴a=1, f(x)=x3-3x
(2)中設切點為(x0,x03-3x0),因為過點A(2,m),所以∴m-(x03-3x0)=(3x02-3)(2-x0)分離參數∴m=-2x03+6x02-6
然后利用g(x)=-2x3+6x2-6函數求導數,判定單調性,從而得到要是有三解,則需要滿足-6<m<2
解:(1)f′(x)=3ax2+2bx+c
依題意
又f′(0)=-3
∴c=-3 ∴a=1 ∴f(x)=x3-3x
(2)設切點為(x0,x03-3x0),
∵f′(x)=3x2-3,∴f′(x0)=3x02-3
∴切線方程為y-(x03-3x0)=(3x02-3)(x-x0)
又切線過點A(2,m)
∴m-(x03-3x0)=(3x02-3)(2-x0)
∴m=-2x03+6x02-6
令g(x)=-2x3+6x2-6
則g′(x)=-6x2+12x=-6x(x-2)
由g′(x)=0得x=0或x=2
∴g(x)在(-∞,0)單調遞減,(0,2)單調遞增,(2,+∞)單調遞減.
∴g(x)極小值=g(0)=-6,g(x)極大值=g(2)=2
畫出草圖知,當-6<m<2時,m=-2x3+6x2-6有三解,
所以m的取值范圍是(-6,2).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com