
 、
、 、
、 }為空間的一組基底,則下列各項中,能構成基底的一組向量是( )
}為空間的一組基底,則下列各項中,能構成基底的一組向量是( ) ,
, +
+ ,
, -
-
 ,
, +
+ ,
, -
-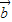
 ,
, +
+ ,
, -
-
 +
+ ,
, -
-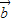 ,
, +2
+2
 +
+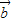 )+(
)+(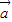 -
-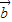 )=2
)=2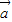 ,∴
,∴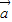 ,
,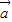 +
+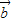 ,
,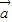 -
-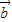 共面,不能構成基底,排除 A;
共面,不能構成基底,排除 A;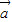 +
+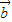 )-(
)-(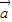 -
-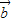 )=2
)=2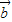 ,∴
,∴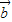 ,
,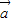 +
+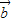 ,
,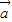 -
-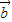 共面,不能構成基底,排除 B;
共面,不能構成基底,排除 B; +2
+2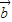 =
= (
(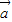 +
+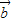 )-
)- (
(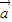 -
-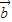 ),∴,
),∴,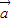 +
+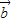 ,
,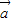 -
-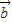 ,
,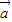 +2
+2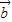 共面,不能構成基底,排除 D;
共面,不能構成基底,排除 D; 、
、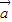 +
+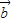 、
、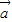 -
-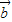 共面,則
共面,則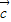 =λ(
=λ(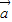 +
+ )+m(
)+m(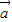 -
-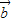 )=(λ+m)
)=(λ+m)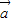 +(λ-m)
+(λ-m)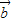 ,則
,則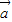 、
、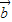 、
、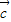 為共面向量,此與{
為共面向量,此與{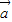 、
、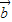 、
、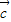 }為空間的一組基底矛盾,故
}為空間的一組基底矛盾,故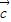 ,
,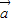 +
+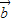 ,
,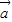 -
- 可構成空間向量的一組基底.
可構成空間向量的一組基底.

科目:高中數學 來源: 題型:
| AB |
| BC |
| CD |
| DA |
| 0 |
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| c |
| a |
| a |
| b |
| c |
| a |
| b |
| c |
| OP |
| OA |
| OB |
| OC |
| A、3 | B、2 | C、1 | D、0 |
查看答案和解析>>
科目:高中數學 來源: 題型:
在下列四個命題中
①已知A、B、C、D是空間的任意四點,則![]() .
.
②若{![]() }為空間的一組基底,則{
}為空間的一組基底,則{![]() }也構成空間的一組基底.
}也構成空間的一組基底.
③![]() .
.
④對于空間的任意一點O和不共線的三點A、B、C,若![]() (其中
(其中![]() ),則P、A、B、C四點共面.
),則P、A、B、C四點共面.
其中正確的個數是 ( )
A.3 A.2 C.1 D.0
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| AB |
| BC |
| CD |
| DA |
| 0 |
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| c |
| a |
| a |
| b |
| c |
| a |
| b |
| c |
| OP |
| OA |
| OB |
| OC |
| A.3 | B.2 | C.1 | D.0 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com