
【題目】已知函數f(x)=x﹣1﹣alnx.
(Ⅰ)若 f(x)≥0,求a的值;
(Ⅱ)設m為整數,且對于任意正整數n,(1+ ![]() )(1+
)(1+ ![]() )…(1+
)…(1+ ![]() )<m,求m的最小值.
)<m,求m的最小值.
【答案】解:(Ⅰ)因為函數f(x)=x﹣1﹣alnx,x>0,
所以f′(x)=1﹣ ![]() =
= ![]() ,且f(1)=0.
,且f(1)=0.
所以當a≤0時f′(x)>0恒成立,此時y=f(x)在(0,+∞)上單調遞增,所以在(0,1)上f(x)<0,這與f(x)≥0矛盾;
當a>0時令f′(x)=0,解得x=a,
所以y=f(x)在(0,a)上單調遞減,在(a,+∞)上單調遞增,即f(x)min=f(a),
又因為f(x)min=f(a)≥0,
所以a=1;
(Ⅱ)由(Ⅰ)可知當a=1時f(x)=x﹣1﹣lnx≥0,即lnx≤x﹣1,
所以ln(x+1)≤x當且僅當x=0時取等號,
所以ln(1+ ![]() )<
)< ![]() ,k∈N*,
,k∈N*,
所以![]() ,k∈N* .
,k∈N* .
一方面,因為 ![]() +
+ ![]() +…+
+…+ ![]() =1﹣
=1﹣ ![]() <1,
<1,
所以,(1+ ![]() )(1+
)(1+ ![]() )…(1+
)…(1+ ![]() )<e;
)<e;
另一方面,(1+ ![]() )(1+
)(1+ ![]() )…(1+
)…(1+ ![]() )>(1+
)>(1+ ![]() )(1+
)(1+ ![]() )(1+
)(1+ ![]() )=
)= ![]() >2,
>2,
同時當n≥3時,(1+ ![]() )(1+
)(1+ ![]() )…(1+
)…(1+ ![]() )∈(2,e).
)∈(2,e).
因為m為整數,且對于任意正整數n(1+ ![]() )(1+
)(1+ ![]() )…(1+
)…(1+ ![]() )<m,
)<m,
所以m的最小值為3.
【解析】(Ⅰ)通過對函數f(x)=x﹣1﹣alnx(x>0)求導,分a≤0、a>0兩種情況考慮導函數f′(x)與0的大小關系可得結論;
(Ⅱ)通過(Ⅰ)可知lnx≤x﹣1,進而取特殊值可知ln(1+ ![]() )<
)< ![]() ,k∈N* . 一方面利用等比數列的求和公式放縮可知(1+
,k∈N* . 一方面利用等比數列的求和公式放縮可知(1+ ![]() )(1+
)(1+ ![]() )…(1+
)…(1+ ![]() )<e;另一方面可知(1+
)<e;另一方面可知(1+ ![]() )(1+
)(1+ ![]() )…(1+
)…(1+ ![]() )>2,且當n≥3時,(1+
)>2,且當n≥3時,(1+ ![]() )(1+
)(1+ ![]() )…(1+
)…(1+ ![]() )∈(2,e).
)∈(2,e).
【考點精析】關于本題考查的利用導數研究函數的單調性和等比數列的前n項和公式,需要了解一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減;前
在這個區間單調遞減;前![]() 項和公式:
項和公式: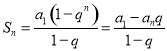 才能得出正確答案.
才能得出正確答案.


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案科目:高中數學 來源: 題型:
【題目】據統計,某地區植被覆蓋面積![]() 公頃
公頃![]() 與當地氣溫下降的度數
與當地氣溫下降的度數![]() 之間呈線性相關關系,對應數據如下:
之間呈線性相關關系,對應數據如下:
| 20 | 40 | 60 | 80 |
| 3 | 4 | 4 | 5 |
![]() 請用最小二乘法求出y關于x的線性回歸方程;
請用最小二乘法求出y關于x的線性回歸方程;
![]() 根據
根據![]() 中所求線性回歸方程,如果植被覆蓋面積為300公頃,那么下降的氣溫大約是多少
中所求線性回歸方程,如果植被覆蓋面積為300公頃,那么下降的氣溫大約是多少![]() ?
?
參考公式:線性回歸方程![]() ;其中
;其中![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=cos(x+ ![]() ),則下列結論錯誤的是( )
),則下列結論錯誤的是( )
A.f(x)的一個周期為﹣2π
B.y=f(x)的圖象關于直線x= ![]() 對稱
對稱
C.f(x+π)的一個零點為x= ![]()
D.f(x)在( ![]() ,π)單調遞減
,π)單調遞減
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】△ABC的內角A,B,C的對邊分別為a,b,c,已知sinA+ ![]() cosA=0,a=2
cosA=0,a=2 ![]() ,b=2.
,b=2.
(Ⅰ)求c;
(Ⅱ)設D為BC邊上一點,且AD⊥AC,求△ABD的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,AB為圓O的直徑,C在圓O上,CF⊥AB于F,點D為線段CF上任意一點,延長AD交圓O于E,∠AEC=30°. 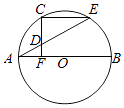
(1)求證:AF=FO;
(2)若CF= ![]() ,求ADAE的值.
,求ADAE的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com