
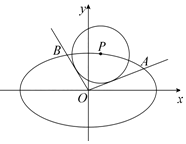
 如圖,已知P(x0,y0)是橢圓C:$\frac{x^2}{4}+{y^2}$=1上一點,過原點的斜率分別為k1,k2的兩條直線與圓(x-x0)2+(y-y0)2=$\frac{4}{5}$均相切,且交橢圓于A,B兩點.
如圖,已知P(x0,y0)是橢圓C:$\frac{x^2}{4}+{y^2}$=1上一點,過原點的斜率分別為k1,k2的兩條直線與圓(x-x0)2+(y-y0)2=$\frac{4}{5}$均相切,且交橢圓于A,B兩點.分析 (1)推導出k1,k2是方程(4-5x02)k2+10x0y0k+4-5y02=0的兩根,由此能利用韋達定理能求出k1k2為定值;
(2)設A(x1,y1),B(x2,y2),聯立$\left\{\begin{array}{l}{y={k}_{1}x}\\{{x}^{2}+4{y}^{2}-4=0}\end{array}\right.$,由此利用橢圓性質,結合已知條件運用基本不等式能求出|OA|•|OB|的最大值.
解答 (1)證明:由圓P與直線OA:y=k1x相切,
可得$\frac{|k{x}_{0}-{y}_{0}|}{\sqrt{1+{{k}_{1}}^{2}}}$=$\frac{2\sqrt{5}}{5}$,
即(4-5x02)k12+10x0y0k1+4-5y02=0,
同理,(4-5x02)k22+10x0y0k2+4-5y02=0,
即有k1,k2是方程(4-5x02)k2+10x0y0k+4-5y02=0的兩根,
可得k1k2=$\frac{4-5{{y}_{0}}^{2}}{4-5{{x}_{0}}^{2}}$=$\frac{-1+\frac{5}{4}{{x}_{0}}^{2}}{4-4{{x}_{0}}^{2}}$=-$\frac{1}{4}$.
(2)解:設A(x1,y1),B(x2,y2),聯立$\left\{\begin{array}{l}{y={k}_{1}x}\\{{x}^{2}+4{y}^{2}-4=0}\end{array}\right.$,
解得x12=$\frac{4}{1+4{{k}_{1}}^{2}}$,y12=$\frac{4{{k}_{1}}^{2}}{1+4{{k}_{1}}^{2}}$,
同理,x22=$\frac{16{{k}_{1}}^{2}}{1+4{{k}_{1}}^{2}}$,y22=$\frac{1}{1+4{{k}_{1}}^{2}}$,
(|OA|•|OB|)2=($\frac{4}{1+4{{k}_{1}}^{2}}$+$\frac{4{{k}_{1}}^{2}}{1+4{{k}_{1}}^{2}}$)•($\frac{16{{k}_{1}}^{2}}{1+4{{k}_{1}}^{2}}$+$\frac{1}{1+4{{k}_{1}}^{2}}$),
∴|OA|•|OB|=2$\sqrt{1+\frac{9{{k}_{1}}^{2}}{16{{k}_{1}}^{4}+8{{k}_{1}}^{2}+1}}$
=2$\sqrt{1+\frac{9}{16{{k}_{1}}^{2}+\frac{1}{{{k}_{1}}^{2}}+8}}$≤$\frac{5}{2}$
當且僅當k1=±$\frac{1}{2}$時,取等號,
可得|OA|•|OB|的最大值為$\frac{5}{2}$.
點評 本題考查兩直線的斜率之積是否為定值的判斷與求法,考查兩線段的最大值的求法,是中檔題,解題時要認真審題,注意橢圓性質、韋達定理、圓的性質的合理運用.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
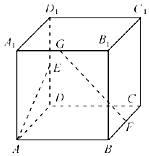 如圖,正方體ABCD-A1B1C1D1中,E、F分別為棱DD1和BC中點G為棱A1B1上任意一點,則直線AE與直線FG所成的角為( )
如圖,正方體ABCD-A1B1C1D1中,E、F分別為棱DD1和BC中點G為棱A1B1上任意一點,則直線AE與直線FG所成的角為( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
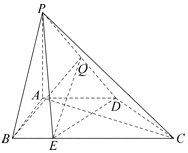 如圖,在四棱錐P-ABCD,PA⊥面ABCD,AD∥BC,AB⊥AD,BC=2AB=2AD=2PA=4BE=4
如圖,在四棱錐P-ABCD,PA⊥面ABCD,AD∥BC,AB⊥AD,BC=2AB=2AD=2PA=4BE=4查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com