
已知函數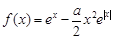 .
.
(Ⅰ)若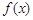 是
是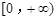 上是增函數,求實數a的取值范圍;
上是增函數,求實數a的取值范圍;
(Ⅱ)證明:當a≥1時,證明不等式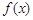 ≤x+1對x∈R恒成立;
≤x+1對x∈R恒成立;
(Ⅲ)對于在(0,1)中的任一個常數a,試探究是否存在x0>0,使得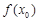 >x0+1成立?如果存在,請求出符合條件的一個x0;如果不存在,請說明理由.
>x0+1成立?如果存在,請求出符合條件的一個x0;如果不存在,請說明理由.
(I)a的取值范圍為a≤0;(Ⅱ)詳見解析;(Ⅲ)可找到一個常數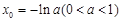 ,使得
,使得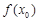 >x0+1成立.
>x0+1成立.
解析試題分析:(I) 時,
時, ,求導得
,求導得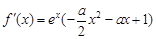 .由題意,
.由題意,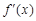 ≥0在
≥0在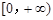 上恒成立.因為ex>0恒成立,故只需
上恒成立.因為ex>0恒成立,故只需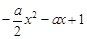 ≥0在
≥0在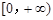 上恒成立,結合拋物線的圖象即可得a的取值范圍;(Ⅱ)由題知f(x)≤x+1即為
上恒成立,結合拋物線的圖象即可得a的取值范圍;(Ⅱ)由題知f(x)≤x+1即為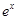 -
-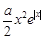 ≤x+1.由于含有
≤x+1.由于含有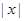 ,故分
,故分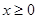 和
和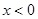 兩種情況討論.①在x≥0時,要證明
兩種情況討論.①在x≥0時,要證明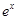 -
-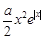 ≤x+1成立,可變為證1≤
≤x+1成立,可變為證1≤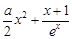 成立,這樣只需利用導數求
成立,這樣只需利用導數求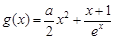 的最小值即可,求導得
的最小值即可,求導得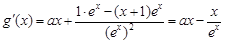 ,易得
,易得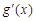 ≥0,從而g(x)≥g(0)=1.注:直接證
≥0,從而g(x)≥g(0)=1.注:直接證 也可,只是需要求兩次導數.
也可,只是需要求兩次導數.
②在x≤0時,要證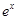 -
-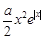 ≤x+1成立,可變為證1≤
≤x+1成立,可變為證1≤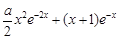 成立,這樣只需利用導數求
成立,這樣只需利用導數求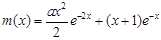 的最小值即可.
的最小值即可.
(Ⅲ)要使f(x0)>x0+1成立,即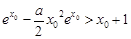 .如果變為
.如果變為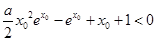 ,那么求導后式子很復雜,故嘗試作其它的變形.
,那么求導后式子很復雜,故嘗試作其它的變形.
變形為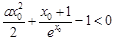 ,要找一個x0>0使該不等式成立,只需找到函數
,要找一個x0>0使該不等式成立,只需找到函數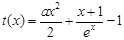 的最小值,滿足
的最小值,滿足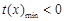 即可.這利用導數就容易解決了.
即可.這利用導數就容易解決了.
試題解析:(I)∵ 時,
時, ,
,
∴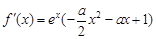 .
.
由題意,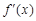 ≥0在
≥0在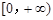 上恒成立,
上恒成立,
當a=0時,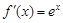 >0恒成立,即滿足條件.
>0恒成立,即滿足條件.
當a≠0時,要使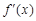 ≥0,而ex>0恒成立,
≥0,而ex>0恒成立,
故只需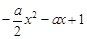 ≥0在
≥0在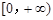 上恒成立,即
上恒成立,即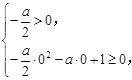 解得a<0.
解得a<0.
綜上,a的取值范圍為a≤0. 4分
(Ⅱ)由題知f(x)≤x+1即為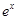 -
-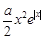 ≤x+1.
≤x+1.
①在x≥0時,要證明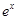 -
-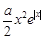 ≤x+1成立,
≤x+1成立,
只需證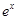 ≤
≤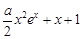 ,即證1≤
,即證1≤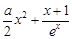 , ①
, ①
令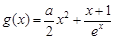 ,得
,得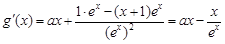 ,
,
整理得 ,
,
∵x≥0時,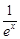 ≤1,結合a≥1,得
≤1,結合a≥1,得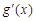 ≥0,
≥0,
∴ 為在
為在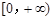 上是增函數,故g(x)≥g(0)=1,從而①式得證.
上是增函數,故g(x)≥g(0)=1,從而①式得證.
②在x≤0時,要使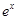 -
-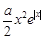 ≤x+1成立,
≤x+1成立,
只需證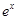 ≤
≤ ,即證1≤
,即證1≤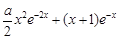 , ②
, ②
令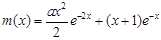 ,得
,得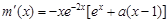 ,
,
而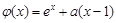 在x≤0時為增函數,
在x≤0時為增函數,
故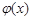 ≤
≤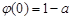 ≤0,從而
≤0,從而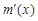 ≤0,
≤0,
∴m(x)在x≤0時為減函數,則m(x)≥m(0)=1,從而②式得證.
綜上所述,原不等式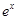 -
-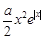 ≤x+1即f(x)≤x+1在a≥1時恒成立. 10分
≤x+1即f(x)≤x+1在a≥1時恒成立. 10分
(Ⅲ)要使f(x0)>x0+1成立,即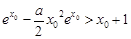 ,
,
變形為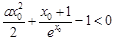 , ③
, ③
要找一個x0>0使③式成立,只


科目:高中數學 來源: 題型:解答題
已知函數f(x)=ln x+ -1.
-1.
(1)求函數f(x)的單調區間;
(2)設m∈R,對任意的a∈(-1,1),總存在x0∈[1,e],使得不等式ma-f(x0)<0成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數
(1)求 的最小值;
的最小值;
(2)設 ,
, .
.
(ⅰ)證明:當 時,
時, 的圖象與
的圖象與 的圖象有唯一的公共點;
的圖象有唯一的公共點;
(ⅱ)若當 時,
時, 的圖象恒在
的圖象恒在 的圖象的上方,求實數
的圖象的上方,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
經調查統計,某種型號的汽車在勻速行駛中,每小時的耗油量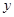 (升)關于行駛速度
(升)關于行駛速度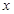 (千米/時)的函數可表示為
(千米/時)的函數可表示為 .已知甲、乙兩地相距
.已知甲、乙兩地相距 千米,在勻速行駛速度不超過
千米,在勻速行駛速度不超過 千米/時的條件下,該種型號的汽車從甲地 到乙地的耗油量記為
千米/時的條件下,該種型號的汽車從甲地 到乙地的耗油量記為 (升).
(升).
(Ⅰ)求函數 的解析式;
的解析式;
(Ⅱ)討論函數 的單調性,當
的單調性,當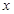 為多少時,耗油量
為多少時,耗油量 為最少?最少為多少升?
為最少?最少為多少升?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
定義在 上的函數
上的函數 同時滿足以下條件:
同時滿足以下條件:
① 在(0,1)上是減函數,在(1,+∞)上是增函數;
在(0,1)上是減函數,在(1,+∞)上是增函數;
② 是偶函數;
是偶函數;
③ 在x=0處的切線與直線
在x=0處的切線與直線 y=x+2垂直.
y=x+2垂直.
(1)求函數 =
= 的解析式;
的解析式;
(2)設g(x)= ,若存在實數x∈[1,e],使
,若存在實數x∈[1,e],使 <
< ,求實數m的取值范圍.
,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲、乙兩地相距1000 ,貨車從甲地勻速行駛到乙地,速度不得超過80
,貨車從甲地勻速行駛到乙地,速度不得超過80 ,已知貨車每小時的運輸成本(單位:元)由可變成本和固定成本組成,可變成本是速度平方的
,已知貨車每小時的運輸成本(單位:元)由可變成本和固定成本組成,可變成本是速度平方的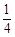 倍,固定成本為a元.
倍,固定成本為a元.
(1)將全程運輸成本y(元)表示為速度v( )的函數,并指出這個函數的定義域;
)的函數,并指出這個函數的定義域;
(2)為了使全程運輸成本最小,貨車應以多大的速度行駛?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com