
在數列![]() 與
與![]() 中,
中,![]() ,數列
,數列![]() 的前
的前![]() 項和
項和![]() 滿足
滿足![]() ,
,![]() 為
為![]() 與
與![]() 的等比中項,
的等比中項,![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求數列![]() 與
與![]() 的通項公式;
的通項公式;
(Ⅲ)設.![]()
![]() 證明:
證明:![]() .
.
(Ⅰ)解:由題設有![]() ,
,![]() ,解得
,解得![]() .由題設又有
.由題設又有![]() ,
,![]() ,解得
,解得![]() .
.
(Ⅱ)解法一:由題設![]() ,
,![]() ,
,![]() ,及
,及![]() ,
,![]() ,進一步可得
,進一步可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
猜想![]() ,
,![]() ,
,![]() .
.
先證![]() ,
,![]() .
.
當![]() 時,
時,![]() ,等式成立.當
,等式成立.當![]() 時用數學歸納法證明如下:
時用數學歸納法證明如下:
(1)當![]() 時,
時,![]() ,等式成立.
,等式成立.
(2)假設![]() 時等式成立,即
時等式成立,即![]() ,
,![]() .
.
![]() 由題設,
由題設,![]()
![]()
①的兩邊分別減去②的兩邊,整理得![]() ,從而
,從而
![]() .
.
這就是說,當![]() 時等式也成立.根據(1)和(2)可知,等式
時等式也成立.根據(1)和(2)可知,等式![]() 對任何的
對任何的![]() 成立.
成立.
綜上所述,等式![]() 對任何的
對任何的![]() 都成立
都成立
再用數學歸納法證明![]() ,
,![]() .
.
(1)當![]() 時,
時,![]() ,等式成立.
,等式成立.
(2)假設當![]() 時等式成立,即
時等式成立,即![]() ,那么
,那么
![]() .
.
這就是說,當![]() 時等式也成立.根據(1)和(2)可知,等式
時等式也成立.根據(1)和(2)可知,等式![]() 對任何的
對任何的![]() 都成立.
都成立.
![]() 解法二:由題設
解法二:由題設![]()
![]()
①的兩邊分別減去②的兩邊,整理得![]() ,
,![]() .所以
.所以
![]() ,
,
![]() ,
,
……
![]() ,
,![]() .
.
將以上各式左右兩端分別相乘,得![]() ,
,
由(Ⅰ)并化簡得![]() ,
,![]() .
.
上式對![]() 也成立.
也成立.
由題設有![]() ,所以
,所以![]() ,
,
即![]() ,
,![]() .
.
令![]() ,則
,則![]() ,即
,即![]() .
.
由![]() 得
得![]() ,
,![]() .所以
.所以![]() ,
,
即![]() ,
,![]() .
.
解法三:由題設有![]() ,
,![]() ,所以
,所以
![]() ,
,
![]() ,
,
……
![]() ,
,![]() .
.
將以上各式左右兩端分別相乘,
得![]() ,化簡得
,化簡得
![]() ,
,![]() .
.
由(Ⅰ),上式對![]() 也成立.所以
也成立.所以![]() ,
,![]() .
.
上式對![]() 時也成立.
時也成立.
以下同解法二,可得![]() ,
,![]() .
.
(Ⅲ)證明:![]() .
.
當![]() ,
,![]() 時,
時,
![]() .
.
注意到![]() ,故
,故
![]()
![]() .
.
當![]() ,
,![]() 時,
時,![]()
當![]() ,
,![]() 時,
時,
![]() .
.
當![]() ,
,![]() 時,
時,
![]() .
.
所以 .
.
從而![]() 時,有
時,有
總之,當![]() 時有
時有![]() ,即
,即![]() .
.


 科學實驗活動冊系列答案
科學實驗活動冊系列答案科目:高中數學 來源:2008年普通高等學校招生全國統一考試理科數學(天津卷) 題型:解答題
(本小題滿分14分)
在數列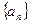 與
與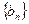 中,
中, ,數列
,數列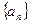 的前
的前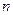 項和
項和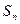 滿足
滿足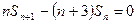 ,
, 為
為 與
與 的等比中項,
的等比中項,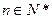 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求數列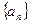 與
與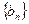 的通項公式;
的通項公式;
(Ⅲ)設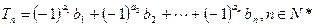 .證明
.證明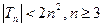 .
.
查看答案和解析>>
科目:高中數學 來源:2008年普通高等學校招生全國統一考試理科數學(天津卷) 題型:解答題
(本小題滿分14分)
在數列 與
與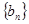 中,
中,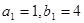 ,數列
,數列 的前
的前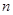 項和
項和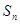 滿足
滿足
 ,
,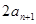 為
為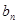 與
與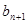 的等比中項,
的等比中項, .
.
(Ⅰ)求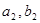 的值;
的值;
(Ⅱ)求數列 與
與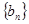 的通項公式;
的通項公式;
(Ⅲ)設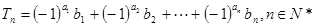 .證明
.證明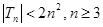 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com