
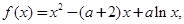 其中常數
其中常數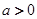 .
.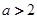 時,求函數
時,求函數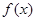 的單調遞增區間;
的單調遞增區間;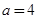 時,若函數
時,若函數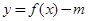 有三個不同的零點,求m的取值范圍;
有三個不同的零點,求m的取值范圍;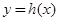 在點
在點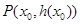 處的切線方程為
處的切線方程為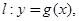 當
當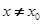 時,若
時,若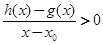 在D內恒成立,則稱P為函數
在D內恒成立,則稱P為函數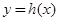 的“類對稱點”,請你探究當
的“類對稱點”,請你探究當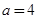 時,函數
時,函數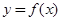 是否存在“類對稱點”,若存在,請最少求出一個“類對稱點”的橫坐標;若不存在,說明理由.
是否存在“類對稱點”,若存在,請最少求出一個“類對稱點”的橫坐標;若不存在,說明理由.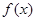 的單調遞增區間為
的單調遞增區間為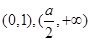 .(2)
.(2)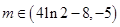 .
.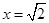 是一個類對稱點的橫坐標.
是一個類對稱點的橫坐標. =
=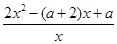 =
=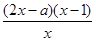
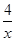 -6,故f′(x)="2x+"
-6,故f′(x)="2x+" 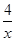 -6≥4
-6≥4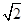 -6,不存在6x+y+m=0這類直線的切線.
-6,不存在6x+y+m=0這類直線的切線. -6)(x-x0)+
-6)(x-x0)+ 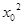 -6x0+4lnx0,令h(x)=f(x)-g(x),由此入手,能夠求出一個“類對稱點”的橫坐標.
-6x0+4lnx0,令h(x)=f(x)-g(x),由此入手,能夠求出一個“類對稱點”的橫坐標.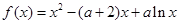 可知,函數的定義域為
可知,函數的定義域為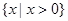 ,
,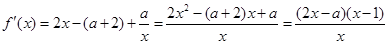 .
.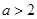 ,所以
,所以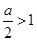 .
.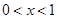 或
或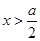 時,
時,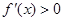 ;當
;當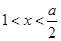 時,
時,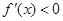 ,
,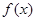 的單調遞增區間為
的單調遞增區間為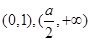 .
.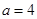 時,
時,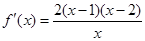 .
.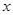 變化時,
變化時,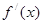 ,
,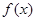 的變化情況如下:
的變化情況如下: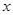 | (0,1) | 1 | (1,2) | 2 | (2,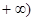 |
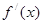 | + | 0 | — | 0 | + |
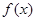 | 單調遞增 | 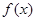 取極大值 取極大值 | 單調遞減 | 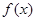 取極小值 取極小值 | 單調遞增 |
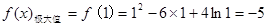 ,
,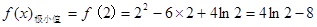 .
.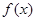 的圖象大致如下:
的圖象大致如下: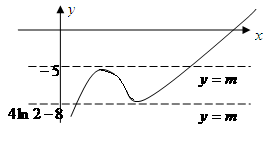
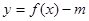 有三個不同的零點,
有三個不同的零點,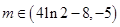 .
.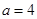 時,
時,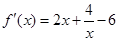 ,則在點P處切線的斜率
,則在點P處切線的斜率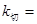
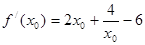 ;所以
;所以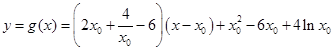
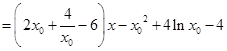 .
.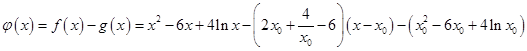 ,
,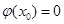 ,
,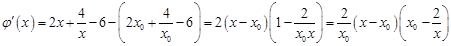 .
.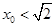 時,
時,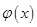 在
在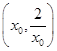 上單調遞減,所以當
上單調遞減,所以當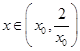 時,
時,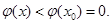 從而有
從而有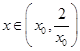 時,
時,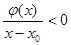 ;
;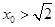 時,
時,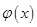 在
在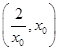 上單調遞減,所以當
上單調遞減,所以當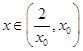 時,
時,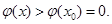 從而有
從而有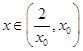 時,
時,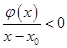 ;所以在
;所以在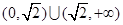 上不存在“類對稱點”.
上不存在“類對稱點”.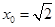 時,
時,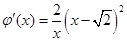 ,所以
,所以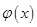 在
在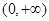 上是增函數,故
上是增函數,故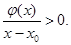
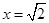 是一個類對稱點的橫坐標.
是一個類對稱點的橫坐標.

 名校課堂系列答案
名校課堂系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com