
本題有2小題,第1小題7分,第2小題7分.
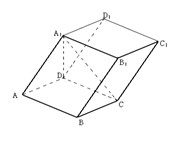 如圖,在平行六面體
如圖,在平行六面體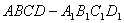 中,
中,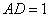 ,
,
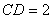 ,
,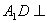 平面
平面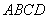 ,
, 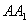 與底面
與底面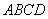 所成
所成
角為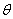 ,
,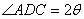 .
.
(1)若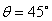 ,求直線
,求直線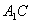 與該平行六面體各側面
與該平行六面體各側面
所成角的最大值;
(2)求平行六面體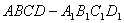 的體積
的體積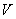 的取值范圍.
的取值范圍.
(1)由平行六面體的性質,知
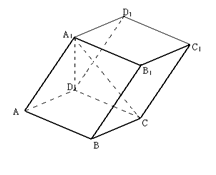 直線
直線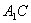 與該平行六面體各側面所成角的大小有兩個,
與該平行六面體各側面所成角的大小有兩個,
其一是直線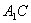 與側面
與側面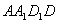 所成角的大小,記為
所成角的大小,記為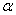 ;
;
其二是直線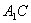 與側面
與側面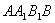 所成角的大小,記為
所成角的大小,記為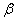 .
.
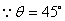 ,
,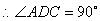 ,即
,即
又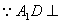 平面
平面 ,
,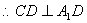
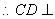 平面
平面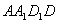 ,
,
所以,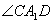 即為所求.……………………………2分
即為所求.……………………………2分
所以,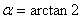 ………………………………1分
………………………………1分
分別以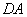 ,
,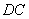 ,
,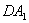 為
為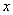 ,
,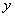 ,
,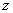 軸建立空間直角坐標系
軸建立空間直角坐標系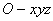 ,
,
可求得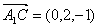 ,側面
,側面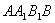 的法向量
的法向量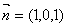 ,
,
所以,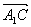 與
與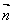 所在直線的夾角為
所在直線的夾角為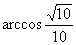
 或
或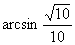 .
.
所以,直線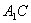 與側面
與側面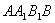 所成角的大小為
所成角的大小為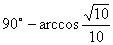 或
或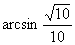 .…3分
.…3分
綜上,直線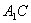 與該平行六面體各側面所成角的最大值為
與該平行六面體各側面所成角的最大值為 .
…………1分
.
…………1分
(2)由已知,有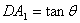 ,
…………………………………………………1分
,
…………………………………………………1分
由面積公式,可求四邊形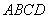 的面積為
的面積為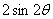 ,…………………………………2分
,…………………………………2分
平行六面體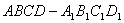 的體積
的體積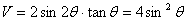 .……………2分
.……………2分
所以,平行六面體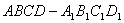 的體積
的體積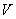 的取值范圍為
的取值范圍為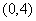 . ……………2分
. ……………2分


 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:高中數學 來源: 題型:
(滿分14分)本題有2小題,第1小題6分,第2小題8分.
已知在平面直角坐標系![]() 中,
中,![]() 三個頂點的直角坐標分別為
三個頂點的直角坐標分別為![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() 為銳角三角形,求
為銳角三角形,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
(滿分14分)本題有2小題,第1小題7分,第2小題7分.
已知在平面直角坐標系![]() 中,
中,![]() 三個頂點的直角坐標分別為
三個頂點的直角坐標分別為![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() 為鈍角,求
為鈍角,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2011屆上海市閘北區(qū)高三第一學期期末數學理卷 題型:解答題
(滿分20分)本題有2小題,第1小題12分,第2小題8分.
已知數列{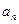 }和{
}和{ }滿足:對于任何
}滿足:對于任何 ,有
,有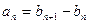 ,
, 為非零常數),且
為非零常數),且 .
.
(1)求數列{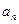 }和{
}和{ }的通項公式;
}的通項公式;
(2)若 是
是 與
與 的等差中項,試求
的等差中項,試求 的值,并研究:對任意的
的值,并研究:對任意的 ,
, 是否一定能是數列{
是否一定能是數列{ }中某兩項(不同于
}中某兩項(不同于 )的等差中項,并證明你的結論.
)的等差中項,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年上海市閘北區(qū)高三第一學期期末數學理卷 題型:解答題
(滿分20分)本題有2小題,第1小題12分,第2小題8分.
已知數列{ }和{
}和{ }滿足:對于任何
}滿足:對于任何 ,有
,有 ,
, 為非零常數),且
為非零常數),且 .
.
(1)求數列{ }和{
}和{ }的通項公式;
}的通項公式;
(2)若 是
是 與
與 的等差中項,試求
的等差中項,試求 的值,并研究:對任意的
的值,并研究:對任意的 ,
, 是否一定能是數列{
是否一定能是數列{ }中某兩項(不同于
}中某兩項(不同于 )的等差中項,并證明你的結論.
)的等差中項,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年上海市閘北區(qū)高三第一學期期末數學理卷 題型:解答題
(滿分15分)本題有2小題,第1小題6分,第2小題9分.
如圖,在直角梯形 中,
中, ,
, ,
, ,
, .將
.將 (及其內部)繞
(及其內部)繞 所在的直線旋轉一周,形成一個幾何體.
所在的直線旋轉一周,形成一個幾何體.
(1)求該幾何體的體積 ;
;

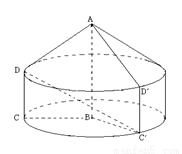 (2)設直角梯形
(2)設直角梯形 繞底邊
繞底邊 所在的直線旋轉角
所在的直線旋轉角 (
( )至
)至 ,問:是否存在
,問:是否存在 ,使得
,使得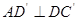 .若存在,求角
.若存在,求角 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.

查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com