
【題目】如圖,在三棱錐![]() 中,
中, ![]() ,
, ![]() 底面
底面![]() ,
, ![]() ,且
,且![]() .
.

(1)若![]() 為
為![]() 上一點,且
上一點,且![]() ,證明:平面
,證明:平面![]() 平面
平面![]() .
.
(2)若![]() 為棱
為棱![]() 上一點,且
上一點,且![]() 平面
平面![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
【答案】(1)見解析;(2)![]()
【解析】試題分析:(1)由![]() 平面
平面![]() 可得
可得![]() ,又
,又![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() ,根據面面垂直的判定定理得平面
,根據面面垂直的判定定理得平面![]() 平面
平面![]() 。(2)在
。(2)在![]() 中,由余弦定理得
中,由余弦定理得
![]() ,根據勾股定理可得AB=3,BC=1,PB=2,由
,根據勾股定理可得AB=3,BC=1,PB=2,由![]() 平面
平面![]() 可得
可得![]() ,從而得到
,從而得到![]() ,故BD=1.過
,故BD=1.過![]() 作
作![]() ,交
,交![]() 于
于![]() ,則
,則![]() 為三棱錐
為三棱錐![]() 的高,且
的高,且![]() 由三棱錐的體積公式可得
由三棱錐的體積公式可得![]() 。
。
試題解析:
(1)證明:∵ ![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
∴![]() .
.
又![]() ,
, ![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴ 平面![]() 平面
平面![]() .
.
(2)解:
在![]() 中,由余弦定理得
中,由余弦定理得
![]() ,
,
∴![]() ,
,
由條件得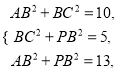 解得
解得 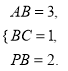
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
∴![]() ,
,
∴![]() .
.
過![]() 作
作![]() ,交img src="http://thumb.zyjl.cn/questionBank/Upload/2017/12/29/18/b0e15a69/SYS201712291828428337502978_DA/SYS201712291828428337502978_DA.053.png" width="28" height="17" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />于
,交img src="http://thumb.zyjl.cn/questionBank/Upload/2017/12/29/18/b0e15a69/SYS201712291828428337502978_DA/SYS201712291828428337502978_DA.053.png" width="28" height="17" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />于![]() ,則
,則![]() 為三棱錐
為三棱錐![]() 的高,則
的高,則![]() .
.
∵![]() ,
,
∴ ![]() .
.
即三棱錐![]() 的體積為
的體積為![]() 。
。


科目:高中數學 來源: 題型:
【題目】學校藝術節對同一類的![]() ,
,![]() ,
,![]() ,
,![]() 四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
甲說:“是![]() 或
或![]() 作品獲得一等獎”;
作品獲得一等獎”;
乙說:“![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“![]() ,
,![]() 兩項作品未獲得一等獎”;
兩項作品未獲得一等獎”;
丁說:“是![]() 作品獲得一等獎”.
作品獲得一等獎”.
若這四位同學中只有兩位說的話是對的,則獲得一等獎的作品是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
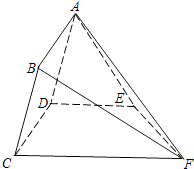
【題目】如圖,矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角,DE∥CF,CD⊥DE,AD=2, ![]() ,CF=6,∠CFE=45°.
,CF=6,∠CFE=45°.
(Ⅰ)求證:BF∥平面ADE;
(Ⅱ)在線段CF上求一點G,使銳二面角B﹣EG﹣D的余弦值為 ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,A,B兩點5條連線并聯,它們在單位時間內能通過的最大信息量依次為2,3,4,3,2.現記從中任取三條線且在單位時間內都通過的最大信息總量為ξ,則P(ξ≥8)= . 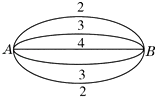
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正四棱錐![]() 中,已知異面直線
中,已知異面直線![]() 與
與![]() 所成的角為
所成的角為![]() ,給出下面三個命題:
,給出下面三個命題:
![]() :若
:若![]() ,則此四棱錐的側面積為
,則此四棱錐的側面積為![]() ;
;
![]() :若
:若![]() 分別為
分別為![]() 的中點,則
的中點,則![]() 平面
平面![]() ;
;
![]() :若
:若![]() 都在球
都在球![]() 的表面上,則球
的表面上,則球![]() 的表面積是四邊形
的表面積是四邊形![]() 面積的
面積的![]() 倍.
倍.
在下列命題中,為真命題的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
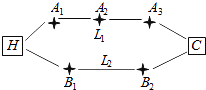
【題目】如圖,李先生家住H小區,他工作在C科技園區,從家開車到公司上班路上有L1、L2兩條路線,L1路線上有A1、A2、A3三個路口,各路口遇到紅燈的概率均為 ![]() ;L2路線上有B1、B2兩個路口,各路口遇到紅燈的概率依次為
;L2路線上有B1、B2兩個路口,各路口遇到紅燈的概率依次為 ![]() ,
, ![]() .
. 
(1)若走L1路線,求最多遇到1次紅燈的概率;
(2)若走L2路線,求遇到紅燈次數X的數學期望;
(3)按照“平均遇到紅燈次數最少”的要求,請你幫助李先生從上述兩條路線中選擇一條最好的上班路線,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD底面是正方形,PA⊥底面ABCD,E,F分別為PA,PD中點. 
(1)求證:EF∥面PBC
(2)求證:平面PBC⊥平面PAB.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com