
設(shè)復(fù)數(shù)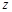 滿足
滿足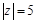 ,且
,且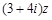 在復(fù)平面上對應(yīng)的點(diǎn)在第二、四象限的角平分線上,
在復(fù)平面上對應(yīng)的點(diǎn)在第二、四象限的角平分線上,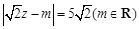 ,求
,求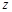 和
和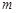 的值.
的值.
 ,
,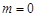 或
或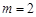 ;或
;或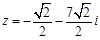 ,
,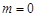 或
或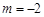 .
.
【解析】
試題分析:設(shè)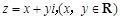 又
又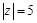 ,
, .
. 1分
1分
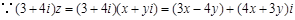 3分
3分
它在復(fù)平面上對應(yīng)的點(diǎn)在第二、四象限的角平分線上, 它的實(shí)部與虛部互為相反數(shù),
它的實(shí)部與虛部互為相反數(shù),
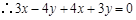 ,即
,即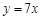 . 5分
. 5分
代入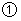 ,得
,得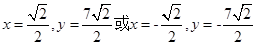 .
.
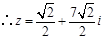 或
或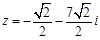 . 7分
. 7分
當(dāng)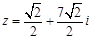 時(shí),
時(shí), 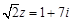 ,依題
,依題 ,即
,即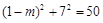 ,
,
解得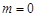 或
或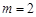 ;
9分
;
9分
當(dāng)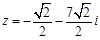 時(shí),
時(shí), 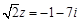 ,同理可解得
,同理可解得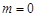 或
或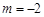 . 11分
. 11分
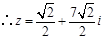 ,
,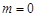 或
或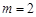 ;或
;或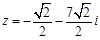 ,
,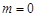 或
或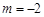 . 12分
. 12分
考點(diǎn):本題考查了復(fù)數(shù)的幾何意義及運(yùn)算
點(diǎn)評:此類問題除了要求學(xué)生掌握復(fù)數(shù)的概念及幾何意義外,還要學(xué)生熟練運(yùn)用復(fù)數(shù)的法則計(jì)算


 超能學(xué)典應(yīng)用題題卡系列答案
超能學(xué)典應(yīng)用題題卡系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
| 3 |
| 2 |
| 2 |
2
| ||
| 3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| 3 |
| 2 |
| 2 |
2
| ||
| 3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
| 3 |
| 2 |
| 2 |
2
| ||
| 3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年上海市浦東新區(qū)高考數(shù)學(xué)二模試卷(文科)(解析版) 題型:解答題
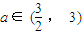 ),當(dāng)n為奇數(shù)時(shí),動點(diǎn)P(x、y)的軌跡為C1.當(dāng)n為偶數(shù)時(shí),動點(diǎn)P(x、y)的軌跡為C2.且兩條曲線都經(jīng)過點(diǎn)
),當(dāng)n為奇數(shù)時(shí),動點(diǎn)P(x、y)的軌跡為C1.當(dāng)n為偶數(shù)時(shí),動點(diǎn)P(x、y)的軌跡為C2.且兩條曲線都經(jīng)過點(diǎn)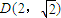 ,求軌跡C1與C2的方程;
,求軌跡C1與C2的方程;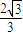 ,求實(shí)數(shù)x的取值范圍.
,求實(shí)數(shù)x的取值范圍.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年上海市浦東新區(qū)高考數(shù)學(xué)二模試卷(理科)(解析版) 題型:解答題
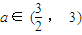 ),當(dāng)n為奇數(shù)時(shí),動點(diǎn)P(x、y)的軌跡為C1.當(dāng)n為偶數(shù)時(shí),動點(diǎn)P(x、y)的軌跡為C2.且兩條曲線都經(jīng)過點(diǎn)
),當(dāng)n為奇數(shù)時(shí),動點(diǎn)P(x、y)的軌跡為C1.當(dāng)n為偶數(shù)時(shí),動點(diǎn)P(x、y)的軌跡為C2.且兩條曲線都經(jīng)過點(diǎn)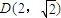 ,求軌跡C1與C2的方程;
,求軌跡C1與C2的方程;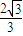 ,求實(shí)數(shù)x的取值范圍.
,求實(shí)數(shù)x的取值范圍.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com