
【題目】已知點![]() 是拋物線
是拋物線![]() 的焦點,點
的焦點,點![]() ,
,![]() 在
在![]() 上,且
上,且![]() .
.
(1)求![]() 的值;
的值;
(2)若直線![]() 經過點
經過點![]() 且與
且與![]() 交于
交于![]() ,
,![]() (異于
(異于![]() )兩點,證明:直線
)兩點,證明:直線![]() 與直線
與直線![]() 的斜率之積為常數.
的斜率之積為常數.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,四棱柱![]() 中,底面
中,底面![]() 是矩形,且
是矩形,且![]() ,
, ![]() ,
, ![]() ,若
,若![]() 為
為![]() 的中點,且
的中點,且![]() .
.
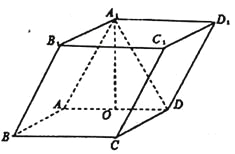
(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)線段![]() 上是否存在一點
上是否存在一點![]() ,使得二面角
,使得二面角![]() 的大小為
的大小為![]() ?若存在,求出
?若存在,求出![]() 的長;若不存在,說明理由.
的長;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C的參數方程為![]() (t為參數),以原點O為極點,x軸的非負半軸為極軸建立極坐標系,過極點的兩射線
(t為參數),以原點O為極點,x軸的非負半軸為極軸建立極坐標系,過極點的兩射線![]() 、
、![]() 相互垂直,與曲線C分別相交于A、B兩點(不同于點O),且
相互垂直,與曲線C分別相交于A、B兩點(不同于點O),且![]() 的傾斜角為銳角
的傾斜角為銳角![]() .
.
(1)求曲線C和射線![]() 的極坐標方程;
的極坐標方程;
(2)求△OAB的面積的最小值,并求此時![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某研究所計劃利用“神舟十號”宇宙飛船進行新產品搭載實驗,計劃搭載新產品甲,乙,要根據該產品的研制成本、產品重量、搭載實驗費用和預計產生收益來決定具體安排,通過調查,有關數據如表:
產品甲(件) | 產品乙(件) | ||
研制成本與搭載費用之和(萬元/件) | 200 | 300 | 計劃最大資金額3000元 |
產品重量(千克/件) | 10 | 5 | 最大搭載重量110千克 |
預計收益(萬元/件) | 160 | 120 |
試問:如何安排這兩種產品的件數進行搭載,才能使總預計收益達到最大,最大收益是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,過
,過![]() 且與
且與![]() 軸垂直的直線被橢圓
軸垂直的直線被橢圓![]() 和圓
和圓![]() 截得的弦長分別為2和
截得的弦長分別為2和![]() .
.
(1)求![]() 的標準方程;
的標準方程;
(2)已知動直線![]() 與拋物線
與拋物線![]() :
:![]() 相切(切點異于原點),且
相切(切點異于原點),且![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點,問:橢圓
兩點,問:橢圓![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() ,若存在求出滿足條件的所有
,若存在求出滿足條件的所有![]() 點的坐標,若不存在,請說明理由.
點的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學擬在高一下學期開設游泳選修課,為了了解高一學生喜歡游泳是否與性別有關,現從高一學生中抽取100人做調查,得到![]() 列聯表:
列聯表:
喜歡游泳 | 不喜歡游泳 | 合計 | |
男生 | 40 | ||
女生 | 30 | ||
合計 | 100 |
且已知在100個人中隨機抽取1人,抽到喜歡游泳的學生的概率為![]() .
.
(1)請完成上面的列聯表;
(2)根據列聯表的數據,是否有99.9%的把握認為喜歡游泳與性別有關?并說明你的理由.
參考公式與臨界值表:![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學在一次研究性學習中發現,以下五個式子的值都等于同一個常數:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() ;
;
⑤![]() ;
;
(1)試從上述五個式子中選擇一個,求出這個常數;
(2)根據(1)的計算結果,將該同學的發現推廣為三角恒等式,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠今年1月、2月、3月生產某產品分別為1萬件、1.2萬件、1.3萬件,為了估計以后每月的產量,以這三個月的產量為依據,用一個函數模擬該產品的月產量,![]() 與月份
與月份![]() 的關系,模擬函數可以選用二次函數或函數
的關系,模擬函數可以選用二次函數或函數![]() 、
、![]() 、
、![]() 為常數)已知四月份該產品的產量為1.37萬件,請問用以上哪個函數作模擬函數較好?說明理由.
為常數)已知四月份該產品的產量為1.37萬件,請問用以上哪個函數作模擬函數較好?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地需要修建一條大型輸油管道通過720千米寬的荒漠地帶,該段輸油管道兩端的輸油站已建好,余下工程只需要在該段兩端已建好的輸油站之間鋪設輸油管道和等距離修建增壓站(又稱泵站).經預算,修建一個增壓站的工程費用為108萬元,鋪設距離為![]() 千米的相鄰兩增壓站之間的輸油管道費用為
千米的相鄰兩增壓站之間的輸油管道費用為![]() 萬元.設余下工程的總費用為
萬元.設余下工程的總費用為![]() 萬元.
萬元.
(1)試將![]() 表示成關于
表示成關于![]() 的函數;
的函數;
(2)需要修建多少個增壓站才能使總費用![]() 最小?
最小?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com