
���}Ŀ����֪��������![]() ��
�� ![]() ��
��![]() �����c(di��n)��
�����c(di��n)��
���C����1��![]() ƽ��
ƽ��![]() ��
��
��2��ƽ��![]() ƽ��
ƽ��![]() ��
��
���𰸡���1��Ҋ(ji��n)������2��Ҋ(ji��n)����
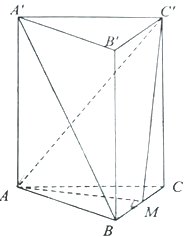
��������ԇ�}��������1���B��![]() ����
����![]() ���c(di��n)
���c(di��n)![]() ���B�Y(ji��)
���B�Y(ji��)![]() �������������|(zh��)�ɵ��c(di��n)
�������������|(zh��)�ɵ��c(di��n)![]() ��
��![]() �����c(di��n)������(j��)��������λ�������ɵ�
�����c(di��n)������(j��)��������λ�������ɵ�![]() �����þ���ƽ�е��ж������ɵ�
�����þ���ƽ�е��ж������ɵ�![]() ƽ��
ƽ��![]() ����2���������������|(zh��)�ɵ�
����2���������������|(zh��)�ɵ�![]() ƽ��
ƽ��![]() ������
������![]() �������������ε����|(zh��)�ɵ�
�������������ε����|(zh��)�ɵ�![]() ������(j��)���洹ֱ���ж������ɵ�
������(j��)���洹ֱ���ж������ɵ�![]() ƽ��
ƽ��![]() ���Ķ�����(j��)���洹ֱ���ж������ɵýY(ji��)Փ.
���Ķ�����(j��)���洹ֱ���ж������ɵýY(ji��)Փ.
ԇ�}��������1���B��![]() ����
����![]() ���c(di��n)
���c(di��n)![]() ���B�Y(ji��)
���B�Y(ji��)![]() ��
��
��?y��n)��������?/span>![]() ��
��
���Ԃ�(c��)��![]() ��ƽ����߅�Σ�
��ƽ����߅�Σ�
���c(di��n)![]() ��
��![]() �����c(di��n)��
�����c(di��n)��
����?y��n)?/span>![]() ��
��![]() �����c(di��n)��
�����c(di��n)��
����![]() ��
��
����?y��n)?/span>![]() ƽ��
ƽ��![]() ��
�� ![]() ƽ��
ƽ��![]() ��
��
����![]() ƽ��
ƽ��![]() ��
��
��2����?y��n)��������?/span>![]() ������
������![]() ƽ��
ƽ��![]() ��
��
����?y��n)?/span>![]() ƽ��
ƽ��![]() ������
������![]() ��
��
��?y��n)��������?/span>![]() ��
�� ![]() ��
��![]() �����c(di��n)��
�����c(di��n)��
![]() ��
��![]() �����c(di��n)������
�����c(di��n)������![]() ��
��
����?y��n)?/span>![]() ������
������![]() ƽ��
ƽ��![]() ��
��
����?y��n)?/span>![]() ƽ��
ƽ��![]() ��
��
����ƽ��![]()
![]() ƽ��
ƽ��![]() ��
��

�������c(di��n)�硿���}��Ҫ���龀��ƽ�е��ж����������洹ֱ�����洹ֱ���C���������Йn�}.�C������ƽ�еij��÷����������þ���ƽ�е��ж�������ʹ���@��(g��)�������P(gu��n)�I���O(sh��)����ƽ���(n��i)�ҵ�һ�l�c��ֱ֪��ƽ�е�ֱ���������Î��w������������������λ������������ƽ�е����|(zh��)���ߘ�(g��u)��ƽ����߅�Ρ����ұ���ʽ�C����ֱ��ƽ��.����������ƽ�е����|(zh��)������ƽ��ƽ�У�������һƽ���(n��i)��ֱ��ƽ������һƽ��. ���}��1���Ǿ������÷������C����.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����![]() ���W(xu��)���ֳ�
���W(xu��)���ֳ�![]() �ɽM���ӳ��оG�����(d��ng)������
�ɽM���ӳ��оG�����(d��ng)������![]() �M����
�M����![]() ���辰��
���辰�� ![]() �M�Nֲ
�M�Nֲ![]() �Ø�(sh��)��.����(j��)�v��y(t��ng)Ӌ(j��)��ÿ���W(xu��)��ÿС�r(sh��)�܉���
�Ø�(sh��)��.����(j��)�v��y(t��ng)Ӌ(j��)��ÿ���W(xu��)��ÿС�r(sh��)�܉���![]() ���辰���߷Nֲ
���辰���߷Nֲ![]() �Ø�(sh��)��.�O(sh��)�����辰�ČW(xu��)����
�Ø�(sh��)��.�O(sh��)�����辰�ČW(xu��)����![]() �ˣ��������辰����Ҫ�ĕr(sh��)�g��
�ˣ��������辰����Ҫ�ĕr(sh��)�g��![]() �������W(xu��)���Nֲ��(sh��)������Ҫ�ĕr(sh��)�g��
�������W(xu��)���Nֲ��(sh��)������Ҫ�ĕr(sh��)�g��![]() ����λ��С�r(sh��)���ɲ�������(sh��)��.
����λ��С�r(sh��)���ɲ�������(sh��)��.
�Ō���![]() ��
��![]() �Ľ���ʽ��
�Ľ���ʽ��
�Ʊ��^![]() ��
��![]() �Ĵ�С���������@
�Ĵ�С���������@![]() ���W(xu��)����ɿ�?c��)΄?w��)�ĕr(sh��)�g
���W(xu��)����ɿ�?c��)΄?w��)�ĕr(sh��)�g![]() �Ľ���ʽ��
�Ľ���ʽ��
�Ǒ�(y��ng)���ӷ���W(xu��)��������ʹ����ɿ�?c��)΄?w��)�ĕr(sh��)�g���٣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�������f(shu��)�������_���ǣ� ��
A. ����![]() �Ќ�(sh��)��
�Ќ�(sh��)��![]() ����(sh��)
����(sh��)![]() �����c(di��n)
�����c(di��n)
B. ![]() �Ѓɂ�(g��)��ͬ�Č�(sh��)��
�Ѓɂ�(g��)��ͬ�Č�(sh��)��
C. ����(sh��)![]() ��
��![]() �ϝM��
�ϝM��![]() ���t
���t![]() ��
��![]() ��(n��i)�����c(di��n)
��(n��i)�����c(di��n)
D. ���{(di��o)����(sh��)�������c(di��n)��������һ��(g��)
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����A={1��3��5��7}��B={x|��2x��1����x��5����0}���tA�ɣ�RB���� ��
A.{1��3}
B.{1��3��5}
C.{3��5}
D.{3��5��7}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)f��x��=x3+ax2+bx�Ѓɂ�(g��)�Oֵ�c(di��n)x1��x2 �� ��x1��x2 �� ��x1+2x0=3x2 �� ����(sh��)g��x��=f��x����f��x0�����tg��x���� ��
A.ǡ��һ��(g��)���c(di��n)
B.ǡ�Ѓɂ�(g��)���c(di��n)
C.ǡ������(g��)���c(di��n)
D.�����ɂ�(g��)���c(di��n)
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ij�N��Ʒ���Ј�(ch��ng)������![]() ���f(w��n)�������Ј�(ch��ng)����(y��ng)��
���f(w��n)�������Ј�(ch��ng)����(y��ng)��![]() ���f(w��n)�����c�Ј�(ch��ng)�r(ji��)��
���f(w��n)�����c�Ј�(ch��ng)�r(ji��)��![]() ��Ԫ/�����քe���Ƶ؝M�������P(gu��n)ϵ��
��Ԫ/�����քe���Ƶ؝M�������P(gu��n)ϵ�� ![]() ��
�� ![]() ����(d��ng)
����(d��ng)![]() �r(sh��)���Ј�(ch��ng)�r(ji��)��Q���Ј�(ch��ng)ƽ��r(ji��)�˕r(sh��)���������Q��ƽ����������
�r(sh��)���Ј�(ch��ng)�r(ji��)��Q���Ј�(ch��ng)ƽ��r(ji��)�˕r(sh��)���������Q��ƽ����������
��1����ƽ��r(ji��)���ƽ����������
��2����ԓ��Ʒ���Ј�(ch��ng)�N����![]() ���f(w��n)�������Ј�(ch��ng)������
���f(w��n)�������Ј�(ch��ng)������![]() ���Ј�(ch��ng)����(y��ng)��
���Ј�(ch��ng)����(y��ng)��![]() �����е��^С�ߣ�ԓ��Ʒ���Ј�(ch��ng)�N���~
�����е��^С�ߣ�ԓ��Ʒ���Ј�(ch��ng)�N���~![]() ���f(w��n)Ԫ�������Ј�(ch��ng)�N����
���f(w��n)Ԫ�������Ј�(ch��ng)�N����![]() �c�Ј�(ch��ng)�r(ji��)��
�c�Ј�(ch��ng)�r(ji��)��![]() �ij˷e��
�ij˷e��
�ٮ�(d��ng)�Ј�(ch��ng)�r(ji��)��![]() ȡ��ֵ�r(sh��)���Ј�(ch��ng)�N���~
ȡ��ֵ�r(sh��)���Ј�(ch��ng)�N���~![]() ȡ�����ֵ��
ȡ�����ֵ��
�ڮ�(d��ng)�Ј�(ch��ng)�N���~![]() ȡ�����ֵ�r(sh��)������ʹ�ô˕r(sh��)���Ј�(ch��ng)�r(ji��)��ǡ�����µ��Ј�(ch��ng)ƽ��r(ji��)�t������(y��ng)ԓ��(du��)ÿ����Ʒ��������Ԫ��
ȡ�����ֵ�r(sh��)������ʹ�ô˕r(sh��)���Ј�(ch��ng)�r(ji��)��ǡ�����µ��Ј�(ch��ng)ƽ��r(ji��)�t������(y��ng)ԓ��(du��)ÿ����Ʒ��������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D����ֱ������![]() �У�����
�У�����![]() �����Σ�
������ ![]() .
.
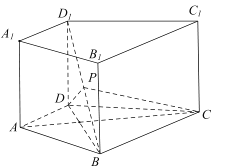
(��)���C�� ![]() ��
��
(��)��![]() ,�c(di��n)
,�c(di��n)![]() �龀��
�龀��![]() �����c(di��n)��Ո(q��ng)?ji��n)ھ���
�����c(di��n)��Ո(q��ng)?ji��n)ھ���![]() ����һ�c(di��n)
����һ�c(di��n)![]() ,ʹ
,ʹ![]() ƽ��
ƽ��![]() �����f(shu��)������.
�����f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
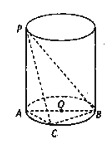
���}Ŀ����D��ʾ, ![]() �LjA����ĸ��,
�LjA����ĸ��, ![]() �LjA������A��ֱ��,
�LjA������A��ֱ��, ![]() �ǵ���A���Ϯ���
�ǵ���A���Ϯ���![]() ������һ�c(di��n),
������һ�c(di��n), ![]() .
.
(1)���C: ![]() ��
��
(2)�������F![]() �w�e�����ֵ,�������˕r(sh��)�����F
�w�e�����ֵ,�������˕r(sh��)�����F![]() �����ı���e.
�����ı���e.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪a��0��b��0����ab=1���t����(sh��)f��x��=ax�c����(sh��)g��x��=��logbx�ĈD������ǣ� ��
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com