
(06年遼寧卷)(14分)
已知點![]() 是拋物線
是拋物線![]() 上的兩個動點,
上的兩個動點,![]() 是坐標原點,向量
是坐標原點,向量![]() 滿足
滿足![]() ,設圓
,設圓![]() 的方程為
的方程為![]() .
.
(1)證明線段![]() 是圓
是圓![]() 的直徑;
的直徑;
(2)當圓![]() 的圓心到直線
的圓心到直線![]() 的距離的最小值為
的距離的最小值為![]() 時,求
時,求![]() 的值.
的值.
解析:(I)證法一:![]()
![]()
即![]()
整理得![]()
![]() ......................12分
......................12分
設點M(x,y)是以線段AB為直徑的圓上的任意一點,則![]()
即![]()
展開上式并將①代入得![]()
故線段![]() 是圓
是圓![]() 的直徑。
的直徑。
證法二:![]()
![]()
即![]() ,
,
整理得![]()
![]() ①……3分
①……3分
若點![]() 在以線段
在以線段![]() 為直徑的圓上,則
為直徑的圓上,則![]()
去分母得![]()
點![]() 滿足上方程,展開并將①代入得
滿足上方程,展開并將①代入得
![]()
所以線段![]() 是圓
是圓![]() 的直徑.
的直徑.
證法三:
![]()
![]()
![]()
即![]() ,
,
整理得![]()
![]()
以![]() 為直徑的圓的方程是
為直徑的圓的方程是![]()
展開,并將①代入得![]()
所以線段![]() 是圓
是圓![]() 的直徑.
的直徑.
(Ⅱ)解法一:設圓![]() 的圓心為
的圓心為![]() ,則
,則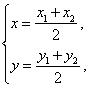
![]() ,
,![]()
又![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
所以圓心的軌跡方程為:![]()
設圓心![]() 到直線
到直線![]() 的距離為
的距離為![]() ,則
,則
![]()
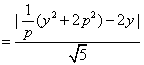
![]()
當![]() 時,
時,![]() 有最小值
有最小值![]() ,由題設得
,由題設得![]()
![]()
![]() ……14分
……14分
解法二:設圓![]() 的圓心為
的圓心為![]() ,則
,則
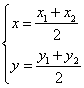
![]()
![]()
又![]()
![]()
![]() …………9分
…………9分
![]()
![]()
![]()
![]()
所以圓心得軌跡方程為![]() …………11分
…………11分
設直線![]() 與
與![]() 的距離為
的距離為![]() ,則
,則![]()
因為![]() 與
與![]() 無公共點.
無公共點.
所以當![]() 與
與![]() 僅有一個公共點時,該點到
僅有一個公共點時,該點到![]() 的距離最小,最小值為
的距離最小,最小值為![]()
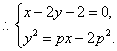
將②代入③![]() ,有
,有
![]() …………14分
…………14分
解法三:設圓![]() 的圓心為
的圓心為![]() ,則
,則
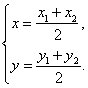
若圓心![]() 到直線
到直線![]() 的距離為
的距離為![]() ,那么
,那么
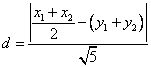
![]()
![]()
又![]()
![]()
![]()
![]()

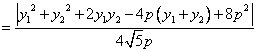
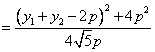
當![]() 時,
時,![]() 有最小值時
有最小值時![]() ,由題設得
,由題設得![]()
![]()


科目:高中數學 來源: 題型:
(06年遼寧卷)(12分)
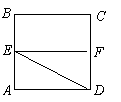
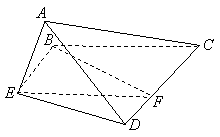
已知正方形![]() ,
,![]() 分別是邊
分別是邊![]() 的中點,將
的中點,將![]() 沿
沿![]() 折起,如圖所示,記二面角
折起,如圖所示,記二面角![]() 的大小為
的大小為![]() (
(![]() ).
).
(1)證明![]() 平面
平面![]() ;
;
(2)若![]() 為正三角形,試判斷點
為正三角形,試判斷點![]() 在平面
在平面![]() 內的射影
內的射影![]() 是否在直線
是否在直線![]() 上,證明你的結論,并求角
上,證明你的結論,并求角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
(06年遼寧卷文)(12分)
已知函數![]() ,
,![]() ,其中
,其中![]() ,設
,設![]() 為
為![]() 的極小值點,
的極小值點,![]() 為
為![]() 的極值點,
的極值點,![]() ,并且
,并且![]() ,將點
,將點![]() 依次記為
依次記為![]() .
.
(1)求![]() 的值;
的值;
(2)若四邊形![]() 為梯形且面積為1,求
為梯形且面積為1,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com