解:(1)由
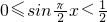
,得:
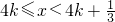
或
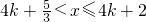
(k∈Z),
由
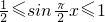
,得:
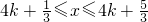
(k∈Z).
所以,函數
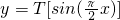
=
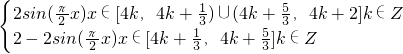
,
函數

=
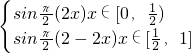
,
所以,
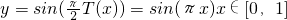
.
(2)
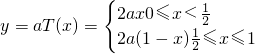
,
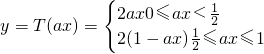
.
當a=0時,則有a(T(x))=T(ax)=0恒成立.
當a>0時,當且僅當a=1時有a(T(x))=T(ax)=T(x)恒成立.
綜上可知當a=0或a=1時,a(T(x))=T(ax)恒成立;
(3)①當
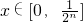
時,對于任意的正整數i∈N
*,1≤i≤n-1,
都有
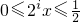
,
故有
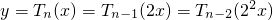
=
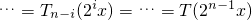
=2
nx.
②由①可知當
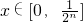
時,有
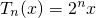
,根據命題的結論可得,
當
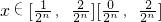
時,有

,
故有
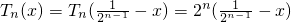
=-2
nx+2.
因此同理歸納得到,當
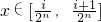
(i∈N,0≤i≤2
n-1)時,

=

.
對于給定的正整數m,當
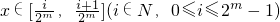
時,
解方程T
m(x)=kx得,
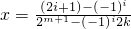
,
要使方程T
m(x)=kx在x∈[0,1]上恰有2
m個不同的實數根,
對于任意i∈N,0≤i≤2
m-1,必須
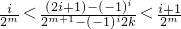
恒成立,
解得
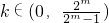
,若將這些根從小到大排列組成數列{x
n},
由此可得
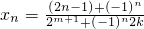
(n∈N
*,1≤i≤2
m).
故數列{x
n}所有2
m項的和為:

=
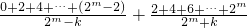
=
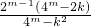
.
分析:(1)由
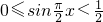
和
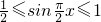
,解出x的范圍,然后直接把
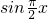
代入分段函數解析式即可,
求y=sin(

T(x))的解析式可把T(x)直接代入.
(2)分別寫出函數y=aT(x)和y=T(ax)的解析式,由解析式看出當a=0時aT(x)=T(ax)恒成立,
而a>0時,直接由aT(x)=T(ax)看出a取1時此等式成立;
(3)①當x∈[0,

]時,x∈[0,

),則在函數T(x)=2x的解析式中,依次取x=2x可求y=T
n(x)的解析式;
②根據題目給出的條件:當x∈[
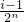
,
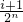
](i∈N
*,1≤i≤2
n-1)時,都有T
n(x)=T
n(
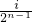
-x)恒成立,
求出當
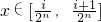
(i∈N,0≤i≤2
n-1)時的T
n(x)的解析式,再由方程T
m(x)=kx求得當
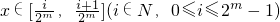
時,
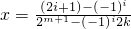
,那么,數列{x
n}所有2
m項的和可利用分組進行求和.
點評:本題考查了函數解析式的求解及常用方法,考查了函數恒成立問題,考查了數列的函數特性及數列的分組求和,特別是(3)中的②涉及到復雜條件下的函數解析式的求解及方程根的問題,需要學生有清晰的頭腦,考查了學生進行復雜運算的能力,此題是難度較大的題目.

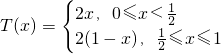
 x))和y=sin(
x))和y=sin( T(x))的解析式;
T(x))的解析式; ]時,求y=Tn(x)的解析式;
]時,求y=Tn(x)的解析式;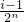 ,
,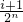 ](i∈N*,1≤i≤2n-1)時,都有Tn(x)=Tn(
](i∈N*,1≤i≤2n-1)時,都有Tn(x)=Tn(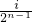 -x)恒成立.
-x)恒成立.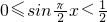 ,得:
,得: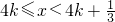 或
或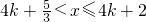 (k∈Z),
(k∈Z),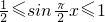 ,得:
,得: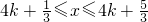 (k∈Z).
(k∈Z).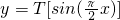 =
=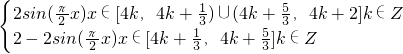 ,
, =
=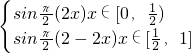 ,
,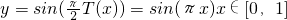 .
.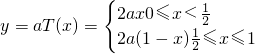 ,
,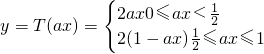 .
.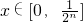 時,對于任意的正整數i∈N*,1≤i≤n-1,
時,對于任意的正整數i∈N*,1≤i≤n-1,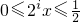 ,
,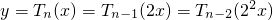 =
=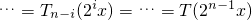 =2nx.
=2nx.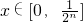 時,有
時,有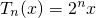 ,根據命題的結論可得,
,根據命題的結論可得,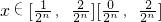 時,有
時,有 ,
,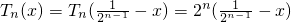 =-2nx+2.
=-2nx+2.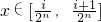 (i∈N,0≤i≤2n-1)時,
(i∈N,0≤i≤2n-1)時, =
= .
.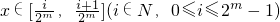 時,
時,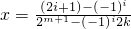 ,
,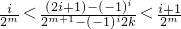 恒成立,
恒成立,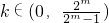 ,若將這些根從小到大排列組成數列{xn},
,若將這些根從小到大排列組成數列{xn},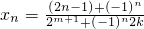 (n∈N*,1≤i≤2m).
(n∈N*,1≤i≤2m).
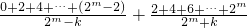
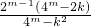 .
.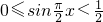 和
和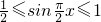 ,解出x的范圍,然后直接把
,解出x的范圍,然后直接把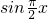 代入分段函數解析式即可,
代入分段函數解析式即可, T(x))的解析式可把T(x)直接代入.
T(x))的解析式可把T(x)直接代入. ]時,x∈[0,
]時,x∈[0, ),則在函數T(x)=2x的解析式中,依次取x=2x可求y=Tn(x)的解析式;
),則在函數T(x)=2x的解析式中,依次取x=2x可求y=Tn(x)的解析式;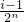 ,
,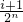 ](i∈N*,1≤i≤2n-1)時,都有Tn(x)=Tn(
](i∈N*,1≤i≤2n-1)時,都有Tn(x)=Tn(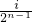 -x)恒成立,
-x)恒成立,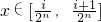 (i∈N,0≤i≤2n-1)時的Tn(x)的解析式,再由方程Tm(x)=kx求得當
(i∈N,0≤i≤2n-1)時的Tn(x)的解析式,再由方程Tm(x)=kx求得當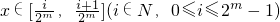 時,
時,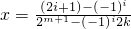 ,那么,數列{xn}所有2m項的和可利用分組進行求和.
,那么,數列{xn}所有2m項的和可利用分組進行求和.

 閱讀快車系列答案
閱讀快車系列答案
 x))和y=sin(
x))和y=sin(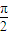 T(x))的解析式;
T(x))的解析式;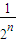 ]時,求y=Tn(x)的解析式;
]時,求y=Tn(x)的解析式;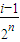 ,
,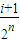 ](i∈N*,1≤i≤2n-1)時,都有Tn(x)=Tn(
](i∈N*,1≤i≤2n-1)時,都有Tn(x)=Tn(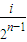 -x)恒成立.
-x)恒成立.
 時,求y=T4(x)的解析式;
時,求y=T4(x)的解析式; 時(i∈N*,1≤i≤15),都有
時(i∈N*,1≤i≤15),都有 恒成立.
恒成立.