
【題目】已知向量 ![]() =(sinθ,﹣2)與
=(sinθ,﹣2)與 ![]() =(1,cosθ)互相垂直,其中θ∈(0,
=(1,cosθ)互相垂直,其中θ∈(0, ![]() ).
).
(Ⅰ)求sinθ和cosθ的值;
(Ⅱ)若sin(θ﹣φ)= ![]() ,0<φ<
,0<φ< ![]() ,求cosφ的值.
,求cosφ的值.
【答案】解:(Ⅰ)∵ ![]() 與
與 ![]() 互相垂直,則
互相垂直,則 ![]() , 即sinθ=2cosθ,代入sin2θ+cos2θ=1得
, 即sinθ=2cosθ,代入sin2θ+cos2θ=1得 ![]() ,又
,又 ![]() ,
,
∴ ![]()
(Ⅱ)∵0<φ< ![]() ,
, ![]() ,
,
∴﹣ ![]() <θ﹣φ<
<θ﹣φ< ![]() ,則cos(θ﹣φ)=
,則cos(θ﹣φ)= ![]() =
= ![]() ,
,
∴cosφ=cos[θ﹣(θ﹣φ)]=cosθcos(θ﹣φ)+sinθsin(θ﹣φ)= ![]()
【解析】(Ⅰ)根據兩向量垂直,求得sinθ和cosθ的關系代入sin2θ+cos2θ=1中求得sinθ和cosθ的值.(Ⅱ)先利用φ和θ的范圍確定θ﹣φ的范圍,進而利用同角三角函數基本關系求得cos(θ﹣φ)的值,進而利用cosφ=cos[θ﹣(θ﹣)]根據兩角和公式求得答案.
【考點精析】解答此題的關鍵在于理解同角三角函數基本關系的運用的相關知識,掌握同角三角函數的基本關系:![]()
![]() ;
;![]()
![]() ;(3) 倒數關系:
;(3) 倒數關系:![]() .
.


科目:高中數學 來源: 題型:
【題目】甲、乙兩位學生參加數學競賽培訓.現分別從他們在培訓期間參加的若干次預賽成績中隨機抽取5次,記錄如下:
甲 | 88 | 89 | 92 | 90 | 91 |
乙 | 84 | 88 | 96 | 89 | 93 |
(Ⅰ)用莖葉圖表示這兩組數據;
(Ⅱ)現要從中選派一人參加數學競賽,你認為選派哪位學生參加合適?請說明理由.(用樣本數據特征來說明.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中 ①若loga3>logb3,則a>b;
②函數f(x)=x2﹣2x+3,x∈[0,+∞)的值域為[2,+∞);
③設g(x)是定義在區間[a,b]上的連續函數.若g(a)=g(b)>0,則函數g(x)無零點;
④函數 ![]() 既是奇函數又是減函數.
既是奇函數又是減函數.
其中正確的命題有
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]()
(1)討論函數![]() 的單調性;
的單調性;
(2)若![]() 有兩個極值點
有兩個極值點![]() ,記過點
,記過點![]() 的直線的斜率為
的直線的斜率為![]() ,問:是否存在實數
,問:是否存在實數![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,點A(0,3),直線l:y=2x﹣4.設圓C的半徑為1,圓心在l上. 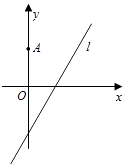
(1)若圓心C也在直線y=x﹣1上,過點A作圓C的切線,求切線的方程;
(2)若圓C上存在點M,使MA=2MO,求圓心C的橫坐標a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}是等差數列,若a9+3a11<0,a10a11<0,且數列{an}的前n項和Sn有最大值,那么Sn取得最小正值時n等于( )
A.20
B.17
C.19
D.21
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知直線![]() 的參數方程為
的參數方程為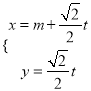 (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,曲線
軸正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,且曲線
,且曲線![]() 的左焦點
的左焦點![]() 在直線上.
在直線上.
(1)若直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值;
的值;
(2)設曲線![]() 的內接矩形的周長為
的內接矩形的周長為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列an的首項a1=2,且an=2an﹣1﹣1(nN+ , n≥2).
(1)求數列{an}的通項公式;
(2)求數列{nan﹣n}的前n項和Sn .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com